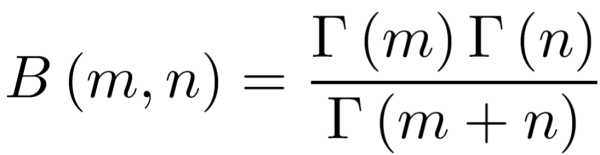少し前に\(\Gamma\)関数についてお話しました。
→ガンマ関数についてのお話~階乗の一般化~
そこではいわゆる階乗(!のやつ)の一般化として\(\Gamma\)関数を定義しました。ここではもう少し進んで2つの整数を組み合わせて考えてみましょう。
以下のような流れで説明していきます。ご自分のご興味に合わせて読んでみて下さい\(^^)/
ステップ1~階乗を2つ掛け算してみよう~
ここでは2つの整数\(m,n\)の階乗の掛け算を考えてみます。
以前お話した\(\Gamma\)関数と階乗のつながりを考えると
\(\begin{eqnarray}
m ! n ! &=& \Gamma\left(m+1\right)\Gamma\left(n+1\right) \\
&=& \int_{0}^{\infty}t^{m}{\rm e}^{-t}{\rm d}t\int_{0}^{\infty}s^{n}{\rm e}^{-s}{\rm d}s \\
&=& \int_{0}^{\infty}\int_{0}^{\infty}{\rm d}t{\rm d}s \,t^{m}s^{n}{\rm e}^{-\left(t+s\right)}\end{eqnarray}\)
となります。指数の肩がいい感じなので変数変換 \(t=x^{2},\,s=y^{2}\)を考えます。このとき\({\rm d}t=2x{\rm d}x,\,{\rm d}s=2t{\rm d}y\) となるから
\(\begin{eqnarray}m ! n ! &=& \int_{0}^{\infty}\int_{0}^{\infty}2x{\rm d}x2y{\rm d}y\,x^{2m}y^{2n}{\rm e}^{-\left(x^{2}+y^{2}\right)} \\
&=& 2\cdot 2\int_{0}^{\infty}\int_{0}^{\infty}{\rm d}x{\rm d}y\,x^{2m+1}y^{2n+1}{\rm e}^{-\left(x^{2}+y^{2}\right)}\end{eqnarray}\)
\(x=r{\rm cos}\theta,\,y=r{\rm sin}\theta\)とすると
\(\begin{eqnarray} m! n! &=& 2\cdot 2\int_{0}^{\infty}r{\rm d}r\int_{0}^{\pi/4}{\rm d}\theta\left(r{\rm cos}\theta\right)^{2m+1}\left(r{\rm sin}\theta\right)^{2n+1}{\rm e}^{-r^{2}}\\
&=& 2\cdot 2\int_{0}^{\infty}r{\rm d}r\int_{0}^{\pi/4}{\rm d}\theta \,r^{2\left(m+n+1\right)}{\rm cos}^{2m}\theta\,{\rm sin}^{2n}\theta\,{\rm e}^{-r^{2}} \\
&=& 2\cdot \underbrace{2\int_{0}^{\infty}{\rm d}r\,r^{2\left(m+n+1\right)+1}{\rm e}^{-r^{2}}}_{=\left(m+n+1\right)!}\int_{0}^{\pi/4}{\rm d}\theta\,{\rm cos}^{2m}\theta\,{\rm sin}^{2n}\theta\end{eqnarray}\)
ステップ2~なんか見たことある形ですなぁ~
実はこの\(r\)の積分のところは\(\Gamma\)関数になっています;
前回の記事の\(\Gamma\)関数の定義で\(t=x^{2}\)とおくと
(関連記事: ガンマ関数についてのお話~階乗の一般化~
\(\begin{eqnarray}z! &=& \Gamma\left(z+1\right) \\
&=& \int_{0}^{\infty}{\rm d}t\,t^{z}{\rm e}^{-t} \\
&=& \int_{0}^{\infty}2x{\rm d}x\,x^{2z}{\rm e}^{-x^{2}} \\
&=& 2\int_{0}^{\infty}{\rm d}x\,x^{2z+1}{\rm e}^{-x^{2}}
\end{eqnarray}\)
ここで\(z=m+n+1\)とするとバッチリ一致しますね。従って
\(\begin{eqnarray}m! n! &=& 2\left(m+n+1\right)!\int_{0}^{\pi/4}{\rm d}\theta\,\cos^{2m}\theta\,\sin^{2n}\theta\end{eqnarray}\)
ゆえに
\(\begin{eqnarray}2\int_{0}^{\pi/4}{\rm d}\theta\,\cos^{2m}\theta\,\sin^{2n}\theta = \frac{m! n!}{\left(m+n+1\right)!}\end{eqnarray}\)
実はこの左辺が\(\beta\)関数と呼ばれているもので、散乱の問題とかでよく出てきます。
\(\begin{eqnarray}B\left(m+1,n+1\right) &\equiv& 2\int_{0}^{\pi/4}{\rm d}\theta\,\cos^{2m}\theta\,\sin^{2n}\theta \\
&=& \frac{\Gamma\left(m+1\right)\Gamma\left(n+1\right)}{\Gamma\left(m+n+2\right)}
\end{eqnarray}\)
グラフにして見てみよう
\(\begin{eqnarray}B\left(m,n\right) &=& \frac{\Gamma\left(m\right)\Gamma\left(n\right)}{\Gamma\left(m+n\right)} \\
&=& 2\int_{0}^{\pi/4}\,\cos^{2\left(m-1\right)}\theta\,\sin^{2\left(n-1\right)}\theta\,{\rm d}\theta\end{eqnarray}\)
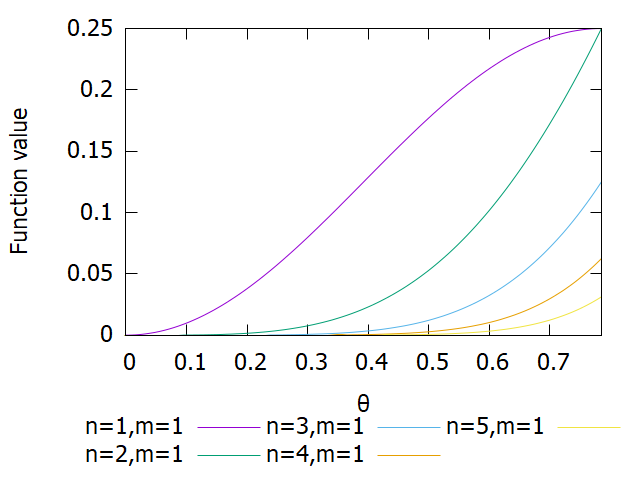
ところでこの被積分関数はどんな形をしているのでしょうか。試しに\(m=1\)で固定しておいて\(n\)をどんどん増やしてみましょう。
 \(\left[0,\pi/4\right]\)で被積分関数をプロットしました
\(\left[0,\pi/4\right]\)で被積分関数をプロットしましたこれを見ると\(n\)が大きくなるにつれて\(\beta\)関数の値は小さくなっていき、なんとなーく0に収束しそうな気がしてきます。
実際、\(\beta\)関数の階乗を使った定義
\(\begin{eqnarray}B\left(m,n\right)=\frac{\left(m-1\right)!\left(n-1\right)!}{\left(m+n-1\right)!}
\end{eqnarray}\)
を見ると、\(m\)を固定して考えれば分母の方が\(n\)が1個だけ多いので整数\(n\rightarrow \infty\)で\(B \simeq\frac{1}{n}\rightarrow 0\)となりますね。
また\(\beta\)関数が\(n\)と\(m\)について対称なので\(m\)を大きくしても同じ結果が得られますね。
ベータ関数関連ではウォリスの公式(Wallis’ formula)など数多くの公式が存在します。この辺についても後々記事にしていこうと思いますので
みなさん、応援よろしくお願いします(^_^)/
まとめ
いかがだったでしょうか。
今回は\(\beta\)関数と\(\Gamma\)関数のつながりについて書いてみました。
レポートなどの参考になれば幸いです。
他にも色々と数学に関することについて書いています。参考にしてみて下さい!
→「数学」一覧
また、\(\Gamma\)関数について書いた記事もあるので合わせて読んでみて下さい!
→ガンマ関数についてのお話~階乗の一般化~
最後まで読んでいただきありがとうございました!!
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。