Hello, guys! It’s me! Warotan!
So…Who are you?→ABOUT ME
I think it very complicated to remember a matrix. right?
Where is the minus sign?
Which comes first, cos or sin?
and so on…
When we have to recall it, for example in test, there is no time to feel easy by proving.
Also in other situation, we can’t be bothered with doing such thing.
For those who are mentioned above, I will tell you an unforgettable way to calculate the matrix!
I think 2d is enough practically, but it can be extended to any dimension with certain polar coordinate definition.
Introduction
What is a rotation matrix?
To begin with, let us consider 2d Cartesian coordinate system.
A rotation matrix is a matrix used to rotate the point \(\left(x,y\right)\) with angle \(\theta\), say \(\left(X,Y\right)\), and represented as follows,
here, \({\bf X} \equiv \left(X,Y\right)^{{\rm T}}\), \({\bf x} \equiv \left(x,y\right)^{{\rm T}}\).
The rotation matrix is the matrix with \(\sin\) and \(\cos\).
The sign is troublesome.
I will introduce a simple verification technique of this.
Polar coordinate
The polar coordinate representation of the point \(\left(x,y\right)\) is
and in the vector form,
\({\bf e}_{x},\,{\bf e}_{y}\) are the basis vectors.
Addition theorem
This is the last part of introduction.
Omitting the proof, but I write the results only as we will use them,
Main part
The general flow is as below,
- Representing the point on the plane with polar coordinate
- Rotating
- Comparing the components with the original
First, we write down the point with polar coordinate
Next, let us rotate with angle \(\alpha\)
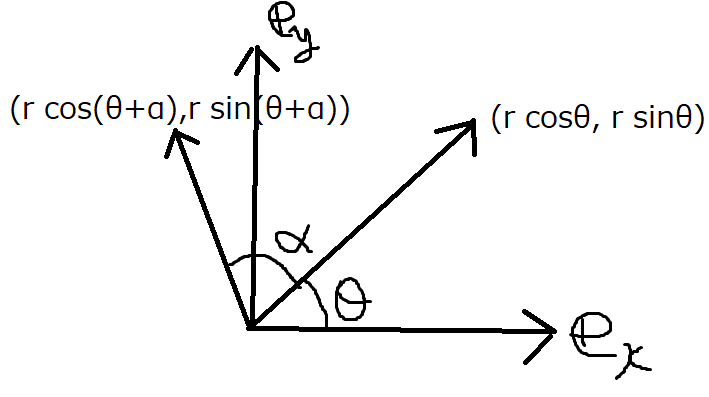
We write the components before rotating as \({\bf x}\), and after as \({\bf X}\).
To get the rotation matrix, we expand \({\bf X}\) as follows.
Therefore,
Summary
Now, that’s all what I wanted to write.
This time I introduced the simple way to remember the rotation matrix.
We can calculate it only if we know the addition theorem.
Thank you for reading and please spread this blog if you like.
If you have any comment, please let me know from the e-mail address below or the CONTACT on the menu bar.
tsunetthi(at)gmail.com
Please change (at) to @.
Or you can also contact me via twitter (@warotan3)



