みなさん、こんにちは!わろたんです!!
私は大学学部時代、卒業研究でシミュレーテッドアニーリング(Simulated Annealing)というシミュレーションを行っていました。これは簡単に言うと、最初に適当な配位を作り、それを揺らしてよりエネルギー的に安定な配位を探し出す方法です。
関連記事: Simulated Annealingってどんな感じ?
今回はこのシミュレーテッドアニーリングという方法を使って、\(\phi^4\) kinkというものを作ってみたので記事にしました!!
細かい計算過程も記してあるので、式変形等で困っている方は読んでみて下さい!!
\(\phi^4\) kinkに入る前にーソリトンって何ぞ???ー
\(\phi^4\) kinkとはソリトンの一種です。ソリトンとは非常に安定な波のことで、川を渡る船の先端から発生する波や光ソリトン通信などが有名ではないでしょうか。
実は船の先っちょから発生する波はソリトン研究の出発点なのです
波の安定性ということをもう少し詳しく見ていくために、こんなことを考えてみます。例えばここに2つのソリトン波があったとしましょう。その2つの波を向い合わせに進行させると、やがて互いに衝突・またはすり抜けます。この衝突の前後で波の振幅がほとんど変わらない、すなわち個々の波がそれぞれ個々の波としてほとんど独立に振る舞っているというのが、ソリトンの特徴です。
\(\phi^4\) kinkって何ぞ???
\(\phi^4\) kinkとはそのようなソリトンの中でも、以下のようなラグランジアン密度を持つオイラーラグランジュ方程式の静的な解です;
ここで、一般性を失わずに\(m>0\)とできます。さて、まずは\(\phi^4\) kinkの満たすオイラーラグランジュ方程式を求めてみましょう。微小量\(\delta\phi\)に対して\(\phi\to\phi+\delta\phi\)という変分を考えます。このとき\(\left(\delta\phi\right)^2\)以上のオーダーの微小量を無視する近似のもと
しかしながら、このオイラーラグランジュ方程式を解かなくても、実はある1階の微分方程式を解けばよいことがわかっています。その方程式とは
です。これはボゴモルニー方程式というものから出てきていて、これについては別記事で説明します。ここではとにかく、そういうものとして話を進めます。
さて、今回の\(\phi^4\) kinkの場合、ポテンシャルの形からしてボゴモルニー方程式は以下のようになります;
この方程式の解は
で与えられることがわかります。 細かい計算はこちら。
→φ^4 kinkの細かい計算
プロットするとこんな感じになってます。
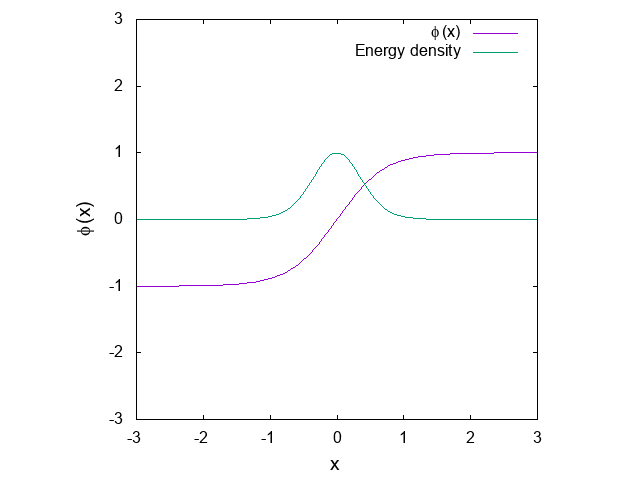
それから、エネルギーの表式は
アニーリングの結果
逆温度\(\beta=1,100\)についてアニーリングを行った結果がこちらになります。
まずはエネルギーから。グラフ中の文字の意味については\(K,\:U,\:E\)の順に
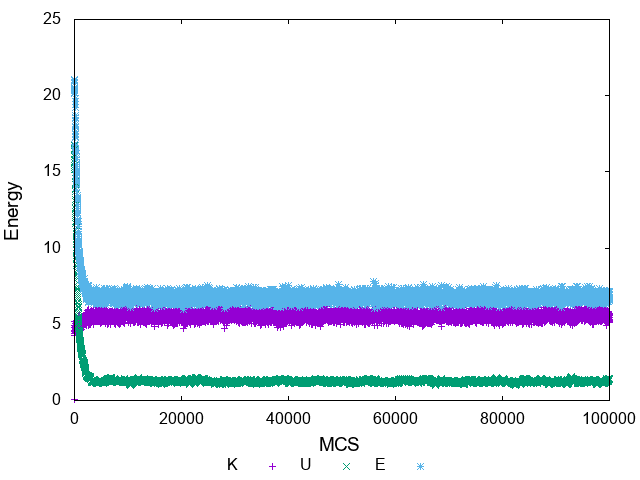
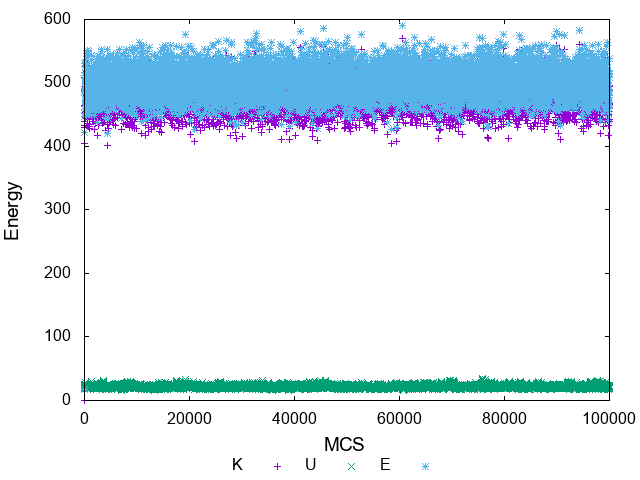
トポロジカルチャージは
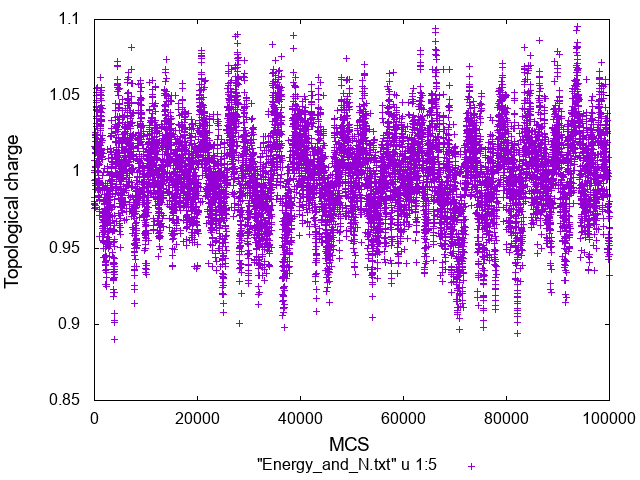
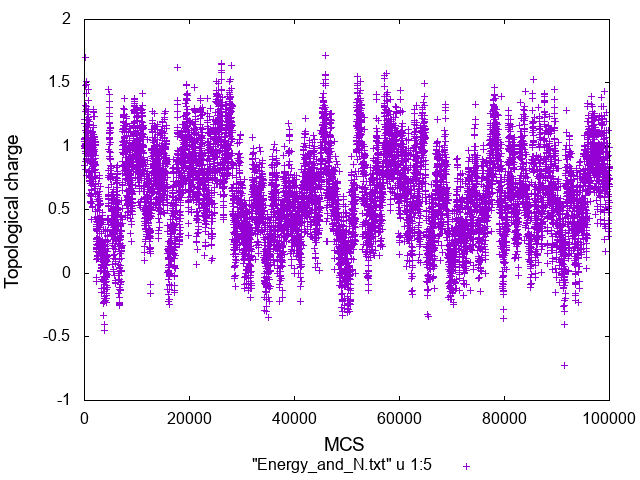
また終状態の配位の様子は
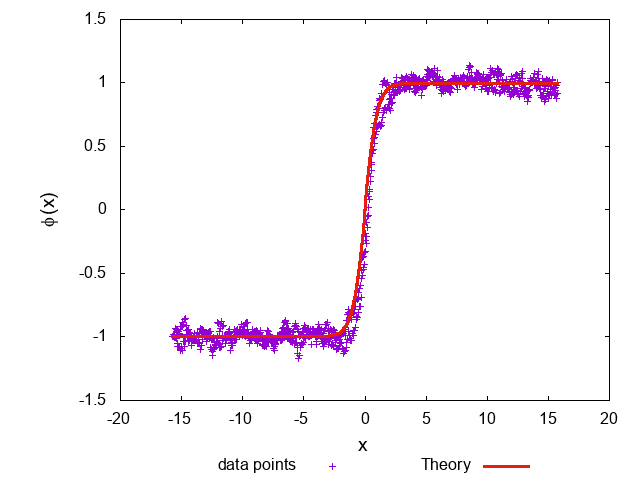
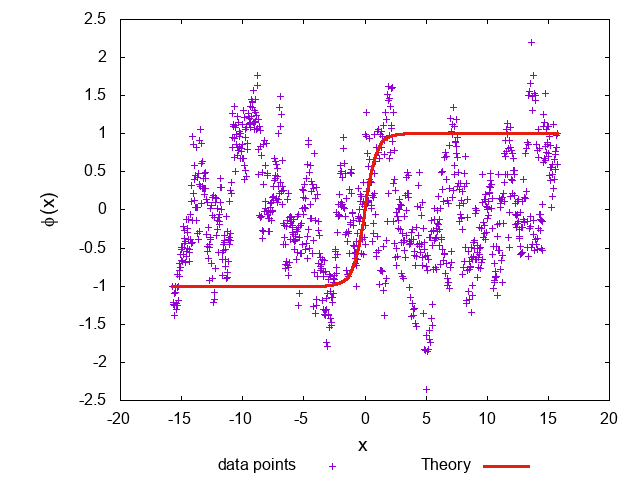
\(\beta=1\)のときは配位が解析解から外れていて、なおかつトポロジカルチャージも保存しておらず、\(\beta=100\)のときは比較的解析解に合っていてトポロジカルチャージもほとんど保存していることから、\(\beta=1\)というのは温度が高すぎてソリトンがほどけてしまっていると考えられる。
結論
見た感じアニーリングは上手くいっているみたい。まっすぐな配位から始めて適当な温度でシミュレーションをすると、きちんと\(\phi^4\) kinkの形が出てきた。
今回記事を書いてみて、色々と忘れていることが多いことが判明したのでその復習をしつつ、最終的にはSkyrme-Faddeevモデルをやりたい。
参考文献
[1] Nicolas Manton & Paul Sutcliffe: Topological Solitons: Cambrige Monographs on Mathematicacl Physics
私が学部時代に読んでいた本です。
洋書なのでなかなか高いですが、もしご興味を持ちましたら読んでみて下さいな。

Topological Solitons (Cambridge Monographs on Mathematical Physics)
最後に
いかがだったでしょうか。今回は\(\phi^4\) kinkのアニーリングの結果を記事にしてみました。
今回の導入のところで使った画像は無料画像提供サイトPixabayさんからダウンロードしました。いつもありがとうございます!(もちろん、シミュレーションの結果のグラフはgnuplotで自分で書いたやつです)
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ下部のコメント欄・上部のお問い合わせフォーム、または下記メールアドレスまでご連絡いただけると大変ありがたいと思います。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。




