空気抵抗ありの落下運動、終端速度とは~自由落下を例として~

今回は空気抵抗ありの落下運動を考えてみましょう。この運動の大事な物理量として終端速度というものを紹介します。

落下運動について
運動方程式と解
運動方程式の解と現実世界との矛盾
空気抵抗を考えてみる
運動方程式と解
終端速度について
終端速度の簡単な求め方
まとめ

落下運動について

まずは落下運動について簡単に復習しましょう。
落下運動とは、「物体が重力の作用で鉛直下向きに行う運動」を言います。(出典: 落下運動（読み）らっかうんどう)

例えば手に持ったボールを初速0で落とすことを考えてみましょう。これは落下運動の中でも自由落下と呼ばれるものであり、高校物理でも一番簡単な落下運動として習います。

運動方程式と解

運動方程式はボールの質量を\(m\)、加速度を\(a\)として、

\(\begin{eqnarray} ma = mg \end{eqnarray}\)

のようになります。積分することにより速度\(v\)と位置\(x\)はそれぞれ

\(\begin{eqnarray} v\left(t\right) &=& gt+v_{0} \\ x\left(t\right) &=& \frac{1}{2}gt^{2}+v_{0}t+x_{0} \end{eqnarray}\)

のように書けます。ここで\(v_{0}\)と\(x_{0}\)はそれぞれ初速度、初期座標です。

いわゆる自由落下の場合、初速\(v_{0} = 0\)です。また、ボールの初期位置を座標系の原点にとり\(x_{0} = 0\)として

\(\begin{eqnarray} v\left(t\right) &=& gt \\ x\left(t\right) &=& \frac{1}{2}gt^{2} \end{eqnarray}\)

となります。

運動方程式の解と現実世界との矛盾

ここで先ほど導いた自由落下の解の性質について少し考えてみましょう。
特に速度について実際にプロットしてみると以下のようになります。

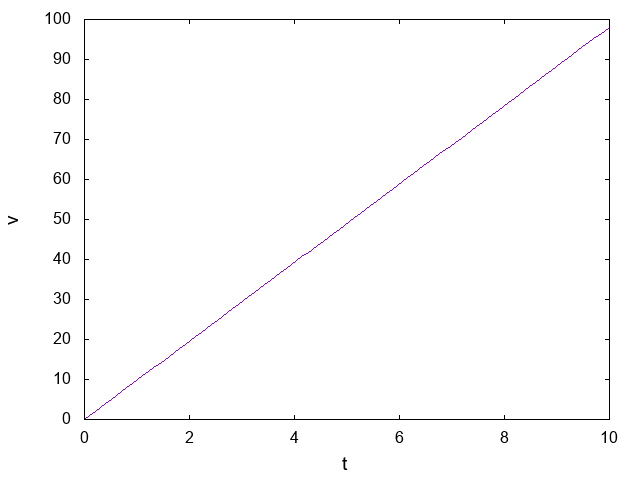
自由落下の速度時間依存性。時間に対し線形。 — 横軸: 時間\(t\)、縦軸: 速度\(v\)

つまり時間とともに速度が際限なく上がっていってしまっています。これは非常に奇妙なことです。
例えば、落下する雨粒は地表付近では 7m/s (25 km/h)ほどと言われていますが(出典: 雨の落ちるスピードはどれくらい)、試しに雨雲の高さ5000mくらいから振ってきた雨の速さを自由落下の式で計算してみると\(v\simeq 313\)m/s (約50 km/h)となって全然合いません。
みなさん、雨足の強い日に傘を忘れて外に出てしまったことが一度や二度はあると思いますが、雨粒が当たっただけでも結構痛いときありますよね。
その40倍近い速度で当たってこられたら一たまりもないのは想像に難くないと思います。そこら中血だらけ、穴だらけです

空気抵抗を考えてみる

自由落下の式だと雨粒などの速度がこれほど遅い説明ができないことが前節までの説明で理解いただけたと思います。
そこで空気抵抗によって速度の上昇が抑えられていると考えてみましょう。
運動する物体の周りに空気があると、空気に引きずられて物体は抵抗を受けます。この効果を運動方程式に取り入れてみましょう。

運動方程式と解

ここでは速度に比例する抵抗を考えてみます。比例係数を\(k\)として運動方程式は

\(\begin{eqnarray} ma = mg-kv \end{eqnarray}\)

となります。自由落下の式と比べると右辺第2項に速度に比例する力の項が追加されています。

この方程式は変数分離形として知られた形であり、容易に解くことができます。加速度\(a = {\rm d}v/{\rm d}t\)であったことを思い出すと、

\(\begin{eqnarray} m\frac{{\rm d}v}{{\rm d}t} &=& mg-kv \\ m\frac{{\rm d}v}{mg-kv} &=& {\rm d}t \\ \frac{{\rm d}v}{v-mg/k} &=& -\frac{k}{m}{\rm d}t \\ \ln\left(v-mg/k\right) &=& -\frac{k}{m}t+C \\ v\left(t\right) &=& C{\rm e}^{-kt/m}+\frac{mg}{k} \end{eqnarray}\)

ここで\(C\)は積分定数です。¹自由落下の場合、\(v|_{t=0} = C+\frac{mg}{k} = 0\)より\(C = -\frac{mg}{k}\)なので最終的な解は

\(\begin{eqnarray} v\left(t\right) &=& \frac{mg}{k}\left(1-{\rm e}^{-kt/m}\right) \end{eqnarray}\)

となります。グラフを描いてみると

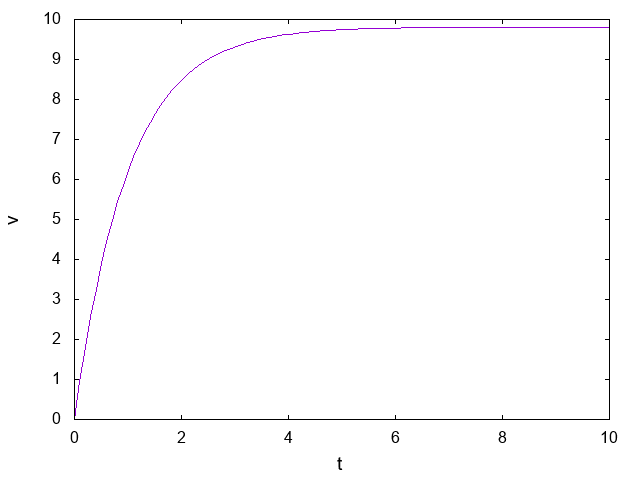
空気抵抗ありの速度時間依存性。時間に対して速度があるところで頭打ちになる。 — 横軸: 時間\(t\)、縦軸: 速度\(v\)

ただし質量、抵抗係数は1にしました。空気抵抗を考慮したことで、速度がどこかで頭打ちになる様子が観察されました。空気抵抗なしの自由落下のときのように時間に対して速度が際限なく早くなるということは起きません。

終端速度について

前節で説明したように空気抵抗を考慮した場合、落下速度はどこかで頭打ちになります。この頭打ちになった速度を「終端速度」と言い、以下のように定義されます。

\(\begin{eqnarray} v_{\infty} \equiv \lim_{t\to\infty}v\left(t\right) \end{eqnarray}\)

速度に比例する空気抵抗を考えている場合、この値は

\(\begin{eqnarray} v_{\infty} = \frac{mg}{k} \end{eqnarray}\)

となります。

終端速度の簡単な求め方

実はこのようなめんどくさい計算をしなくても、終端速度を求めることはできるので最後に紹介します。

終端速度というのは物体にかかる重力と空気抵抗の力が釣り合って一定になったときの速度と考えられるので、\(kv=mg\)より

\(\begin{eqnarray} v = \frac{mg}{k} \end{eqnarray}\)

と求めることもできます。終端速度を求めるだけならこの方が早いですね。一方、途中の速度がどうなるかも知りたいときには微分方程式を真面目に解かないといけません。

まとめ

今回は空気抵抗ありの落下運動と終端速度についてご紹介してみました。
空気抵抗と言えば以下のような記事も書いているので読んでみてね！
関連記事: 無視ばっかりしてんじゃないよ!空気抵抗ありの振り子を考えてみよう！

他にも物理に関することを色々記事にしているので読んでいただけると幸いです！

ちょっと大人な物理たち: 「シミュレーション」一覧

「高校物理」一覧

常微分方程式入門—物理を使うすべての人へ

※ Amazonのアソシエイトとして著者わろたんは適格販売により収入を得ています。

この記事に関するご質問や、もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。

tsunetthi(at)gmail.com

(at)の部分を@に変えてメールをお送りください。

または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。

この記事のサムネイル画像はpixabayさんからダウンロードしました！いつもありがとうございます！

余談ですが、この解き方は対象とする時間スケールで速度が\(mg/k\)を超えないと分かっているときに使えます。例えば初速があったりして一時的に\(mg/k\)を超えるような場合には自然対数の中が負になる時間領域があり、不適になってしまいます。このような場合は別の解の形を仮定して解く方法があり、そのやり方はまた今度ご紹介しようと思います。