以前、高校物理でよく出てくるエネルギーの保存則の話をしました。
エネルギー?保存則?って人はまず以下の記事を読んでみて下さい!
関連記事: 高校物理のお話~エネルギー保存 (基礎編)~
そこでは簡単のために空気抵抗は考えないものとしましたが、現実には空気抵抗がありやがて振り子は止まります。
今回はより現実的な物理を考えてみようということで、空気抵抗も加味した振り子の運動を考えてみましょう。1
とくにどのくらいの時間で振り子が止まるかについてエネルギーの観点から考えてみることにします。
以下のような流れで説明していきます。
また、高校物理に関する記事は以下にまとめてあります。
「高校物理」一覧
他の記事も読んでみて下さい!
それから、空気抵抗関連でこんな記事も書いているので良かったら読んでみてね!
関連記事: 空気抵抗ありの落下運動、終端速度とは~自由落下を例として~
振り子の運動方程式
質量 \(m\)、長さ \(l\)、重力加速度 \(g\)、
張力 \({\bf T}\)、 速度に比例する抵抗 \(mb{\bf v}\)(\({\bf v}\)は速度)のもとで運動する振り子を考えます。2
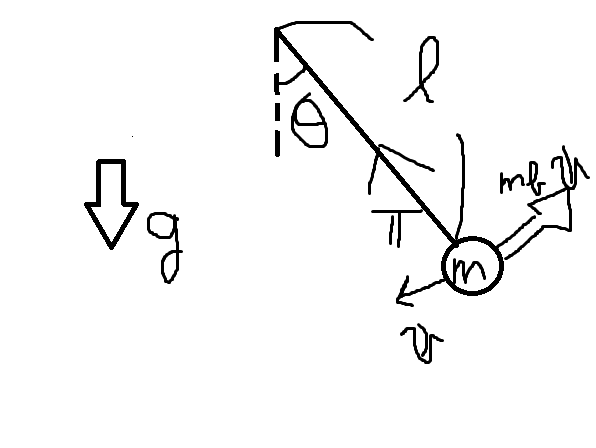

質量 \(m\)、長さ \(l\)、重力加速度 \(g\)、張力 \({\bf T}\)、速度に比例する抵抗 \(mb{\bf v}\)(\({\bf v}\)は速度)のもとで運動する振り子
運動方程式は質点の位置ベクトルを \({\bf r}\)として
基底を定義するのがめんどくさいので、とりあえず全てベクトル表記にしています。あとで基底をしっかり定義して解いていくことにします。
極座標系で解く
のちのちエネルギーに関する考察はしていきますが、そこで運動方程式の解を使うので解が求まるように成分で書いておきます。
位置ベクトルの時間微分
まずは位置ベクトル \({\bf r}\)の時間微分を考えてみましょう。3
と書きます。
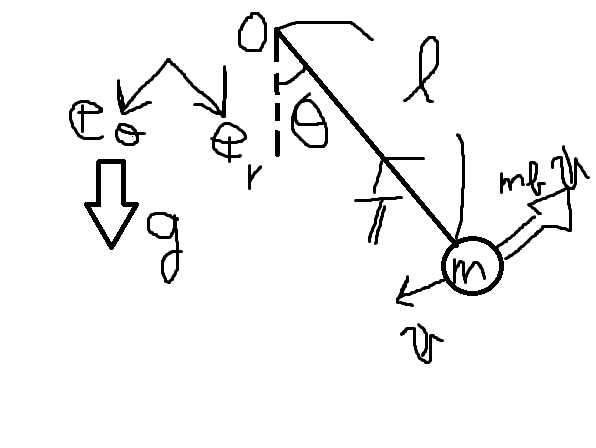


ひもの頂点を原点\(O\)とし、極座標系を定義します。
このとき、\(\dot{{\bf e}}_{r} = \dot{\theta}{\bf e}_{\theta},\,
\dot{{\bf e}}_{\theta} = -\dot{\theta}{\bf e}_{r}\) なので4
ここで \(r = l = {\rm const}\) なので \(\dot{r}=0\) なことを考えれば
ついでに運動方程式右辺の空気抵抗の項に含まれている速度も計算しておくと
になります。
重力の項
重力の項を先ほど定義した極座標系で書きます。鉛直上向きにDescartes 座標系の \(y\) 軸を取ったとすると
と書けます。
張力の項
張力の項は簡単で
ですね。
以上を運動方程式に代入
以上を運動方程式に代入すると \(r,\,\theta\)成分それぞれから
エネルギーの空気抵抗による散逸
エネルギーの表式を導出するためによくやられるように、
ベクトル表記の運動方程式
の両辺に\(\dot{\bf r}\)をかけて




振り子は円運動の一部なので、上図からもわかるように速度と張力ベクトルは常に直交しています。すなわち \({\bf T}\cdot\dot{\bf r} = 0\) が言えます。
また、
なので結局
左辺は力学的エネルギーの時間変化を表していますから、これがエネルギーの散逸を表す方程式だとみることができます。
時間 \(\tau\) で振り子が止まるとすると
最初の振り子の角度を \(\theta_{0}\) とすると


エネルギー保存則導出のもう少し一般的な話はこちら: 力学的エネルギー保存則の導出と例題
振り子が止まるまでの時間を求める
\(\theta\) が非常に小さいときは\(\sin\theta\simeq\theta\)と近似できるので解析的に\(\tau\)を求めることができそうです。
先ほどの
より
すなわち
これは単振動の式であり、解は
ただし \(\omega = \frac{\sqrt{4g/l-b^{2}}}{2} \) 。
あとは時間微分を真面目に計算して \(\tau\) を求めてみましょう!
うーん、なんかもういっかな。
今回の記事で言いたかったのはエネルギー保存から振り子の止まる時間が計算できるよってことでした!
まとめ
いかがだったでしょうか。
今回はエネルギー的な観点から、空気抵抗下での振り子の運動を考えてみました!
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。
- 今回の話は微積をふんだんに使うのでどちらかというと大学生の方向きかもしれません。
- ひもの張力 \({\bf T}\)を忘れがちなので注意しましょう。
- 私の記事では細かい計算もなるべく書いて初学者の方にも抵抗のない記事にしようという考えがあるので、こういうめんどくさい計算も一応載せています。あまりに複雑なものは別記事にしていますが。。。
- \({\bf e}_{r} = \cos\theta{\bf e}_{x}+\sin\theta{\bf e}_{y},\,{\bf e}_{\theta} = -\sin\theta{\bf e}_{x}+\cos\theta{\bf e}_{y}\)と考えることで導くことができます。


