力学的エネルギー保存則の導出と例題

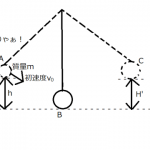
後の記事で使うので、今回は運動方程式からエネルギー保存の式を導出してみようと思います！

関連記事: 無視ばっかりしてんじゃないよ!空気抵抗ありの振り子を考えてみよう！

以下のような流れで説明していきます。

運動方程式に速度をかけて積分
力\(F\)が保存力の場合
(例題) バネのエネルギー保存則の導出
まとめ

運動方程式に速度をかけて積分

質量\(m\)の質点の運動を考えます。簡単のため1次元とします。
運動方程式は\(v\)を速度成分として

\(\begin{eqnarray} m\frac{{\rm d}v}{{\rm d}t} = F \end{eqnarray}\)

です。ここで加速度は\(\frac{{\rm d}v}{{\rm d}t}\)のように書けることに注意してください。

両辺に速度\(v = \frac{{\rm d}x}{{\rm d}t}\)をかけて\(t\)で積分すると

\(\begin{eqnarray} \int m\frac{{\rm d}v}{{\rm d}t} v{\rm d}t &=& \int F v{\rm d}t \\ \int \frac{1}{2}m\frac{{\rm d}}{{\rm d}t}v^2 {\rm d}t &=& \int F \frac{{\rm d}x}{{\rm d}t}{\rm d}t \\ \frac{1}{2}mV^2-\frac{1}{2}mv_{0}^{2} &=& \int F {\rm d}x \end{eqnarray}\)

ここで終状態の速度成分を\(V\), 始状態の速度成分を\(v_{0}\)と書きました。

この最後の等式

\(\begin{eqnarray} \frac{1}{2}mV^2-\frac{1}{2}mv_{0}^{2} = \int F {\rm d}x \end{eqnarray}\)

がエネルギー保存則の式です。

力\(F\)が保存力の場合

力\(F\)が保存力の場合を考えます。
保存力とは上式の積分\(\int F{\rm d}x\)が途中の経路に依らないような力のことです。¹
この場合はポテンシャルエネルギーというエネルギーを定義することが出来ます。

\(\begin{eqnarray} U = \int_{x_{0}}^{x}F{\rm d}x \end{eqnarray}\)

このときエネルギー保存則の式は

\(\begin{eqnarray} \frac{1}{2}mV^2-\frac{1}{2}mv_{0}^{2} = U\left(x\right)-U\left(x_{0}\right) \end{eqnarray}\)

のように書くことができます。
例えばバネのエネルギーや重力のエネルギーなどがこのような形に書くことができます。

(例題) バネのエネルギー保存則の導出

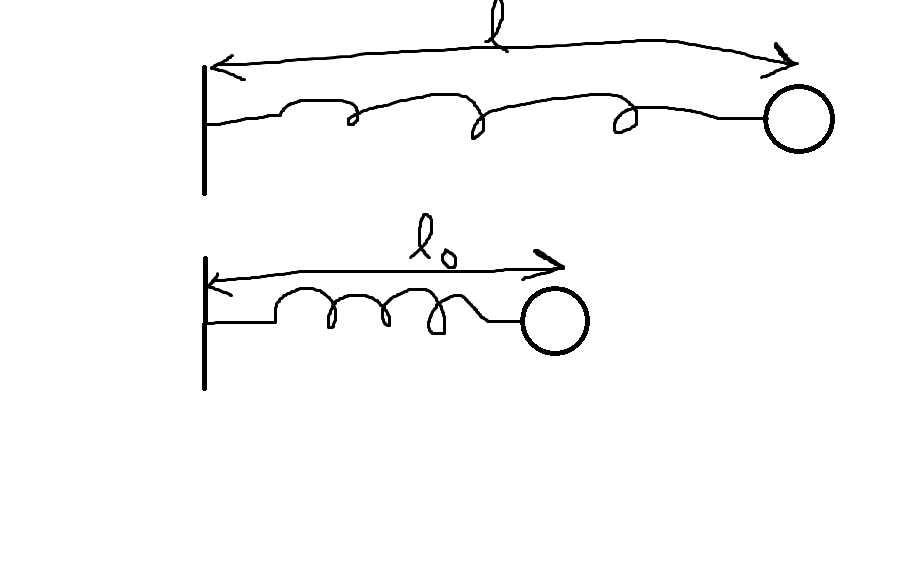
具体的に計算して慣れてもらうために先ほどの式に従ってバネのエネルギー保存則を導出してみましょう。

自然長\(l_{0}\)のバネを長さ\(l\)まで伸ばして初速度0で手を離すことを考えます。バネの先には質量\(m\)の質点が付いているものとします。
このとき、自然長の位置を座標の原点にとれば変位は\(x = l-l_{0} ~ 0\)なのでエネルギー保存則の右辺は

\(\begin{eqnarray} \int F {\rm d}x = \int_{l-l_{0}}^{0}\left(-kx\right){\rm d}x \end{eqnarray}\)

ここでフックの法則からバネの復元力は\(F = -kx\)であることを使いました。
積分を実行すれば

\(\begin{eqnarray} \int_{l-l_{0}}^{0}\left(-kx\right){\rm d}x &=& -\left[\frac{1}{2}kx^{2}\right]_{l-l_{0}}^{0} \\ &=& \frac{1}{2}k\left(l-l_{0}\right)^{2} \end{eqnarray}\)

一方、左辺について考えると初速度は0で、自然長のときの速さを\(v\)と書くと\(-\frac{1}{2}mv^2\)なのでエネルギー保存則より

\(\begin{eqnarray} \frac{1}{2}mv^2 &=& \frac{1}{2}k\left(l-l_{0}\right)^{2} \end{eqnarray}\)

よく見るエネルギー保存則の式が出てきたと思います。