Deriving the energy conservation law and solving an example problem

We will derive the energy conservation law here, as it is used in this article.
-> Let’s think about a pendulum with air resistance

The explanation is as follows.

Integrating the equation of motion with the velocity multiplied
When the force \(F\) is a conservative force
(Example problem) a spring
Summary

Integrating the equation of motion with the velocity multiplied

Let us consider the motion of a mass point with mass \(m\).
We will take a 1 dimensional motion for simplicity.
The equation of motion can be written as

\(\begin{eqnarray} m\frac{{\rm d}v}{{\rm d}t} = F, \end{eqnarray}\)

with \(v\) the velocity component.
Here, note that acceleration is written as \(\frac{{\rm d}v}{{\rm d}t}\).

Multiplying the velocity \(v = \frac{{\rm d}x}{{\rm d}t}\) and integrating with \(t\),

\(\begin{eqnarray} \int m\frac{{\rm d}v}{{\rm d}t} v{\rm d}t &=& \int F v{\rm d}t \\ \int \frac{1}{2}m\frac{{\rm d}}{{\rm d}t}v^2 {\rm d}t &=& \int F \frac{{\rm d}x}{{\rm d}t}{\rm d}t \\ \frac{1}{2}mV^2-\frac{1}{2}mv_{0}^{2} &=& \int F {\rm d}x, \end{eqnarray}\)

we denoted the velocity of the final state as \(V\), and the initial state as \(v_{0}\).

The last equation

\(\begin{eqnarray} \frac{1}{2}mV^2-\frac{1}{2}mv_{0}^{2} = \int F {\rm d}x \end{eqnarray}\)

is the equation of the energy conservation law.

When the force \(F\) is a conservative force

Here, we assume the force \(F\) a conservative force.
The conservative force is a force that the integral \(\int F{\rm d}x\) does NOT depend on the path.
We can define a potential energy

\(\begin{eqnarray} U = \int_{x_{0}}^{x}F{\rm d}x, \end{eqnarray}\)

and the energy conservation equation can be written as

\(\begin{eqnarray} \frac{1}{2}mV^2-\frac{1}{2}mv_{0}^{2} = U\left(x\right)-U\left(x_{0}\right) \end{eqnarray}\)

For example, the energy of a spring or gravity can be provided in this form.

(Example problem) a spring

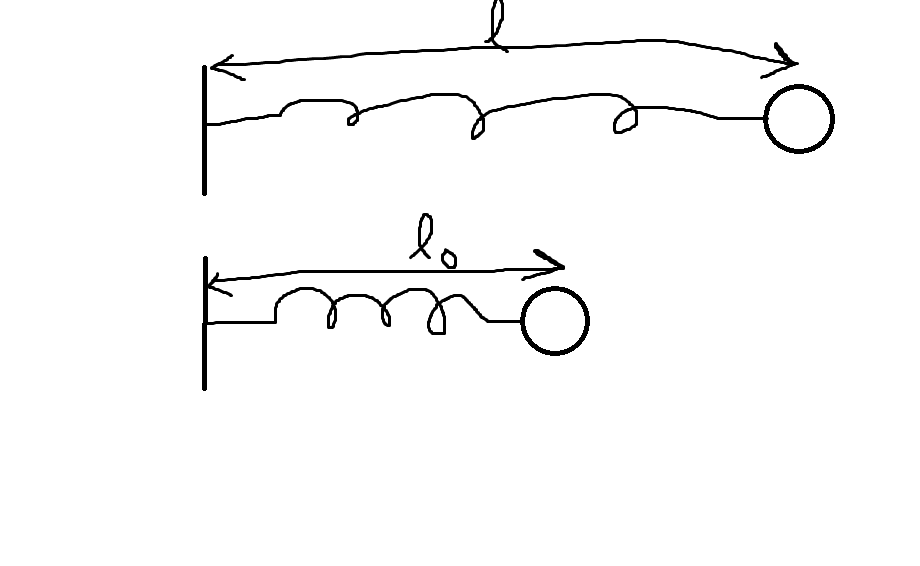
A spring with the equilibrium length \(l_{0}\) stretched to \(l\).

Let’s derive the energy conservation law of a spring to get used to it.

We think about stretching the spring equilibrium length \(l_{0}\) to \(l\) and letting it go with zero initial velocity.
A mass point with mass \(m\) is on the edge.

If we take the origin at the equilibrium position, the displacement is \(x = l-l_{0}\) and the equation of energy conservation is

\(\begin{eqnarray} \int F {\rm d}x = \int_{l-l_{0}}^{0}\left(-kx\right){\rm d}x, \end{eqnarray}\)

here, the resilience is given by \(F = -kx\) by the Hooke’s law.
Integrating this, we get

\(\begin{eqnarray} \int_{l-l_{0}}^{0}\left(-kx\right){\rm d}x &=& -\left[\frac{1}{2}kx^{2}\right]_{l-l_{0}}^{0} \\ &=& \frac{1}{2}k\left(l-l_{0}\right)^{2} \end{eqnarray}\)

On the other hand, as for the left hand side, the initial velocity is 0, and if we write the velocity \(v\) at \(x = 0\), it is given by \(\frac{1}{2}mv^2\).
Using the energy conservation law,

\(\begin{eqnarray} \frac{1}{2}mv^2 &=& \frac{1}{2}k\left(l-l_{0}\right)^{2} \end{eqnarray}\)

This is the common form of the energy conservation equation.

Summary

Now, that’s all what I wanted to write.

This time, we derived the energy conservation equation and solved an example problem.

Thank you for reading and please spread this blog if you like.

If you have any comment, please let me know from the e-mail address below or the CONTACT on the menu bar.
tsunetthi(at)gmail.com
Please change (at) to @.

Or you can also contact me via twitter (@warotan3)