Let’s think about a pendulum with air resistance

I wrote about the conservation law of energy before (English version coming soon), which is often discussed in high school physics.

For simplicity, we didn’t consider the effect of air resistance, but in reality, there is and the pendulum eventually stops.
This time, let’s think about more realistic physics and consider the motion of a pendulum that also takes air resistance into account.
In particular, we will consider how long it takes to stop from the energy point of view.

The equation of motion
Energy dissipation by air resistance
Summary

There are also some articles about physics in high school, so please enjoy them!

The equation of motion

Let’s consider a pendulum with mass \(m\), length \(l\), gravitational acceleration \(g\), tension \(T\), resistance proportional to the velocity \(mb{\bf v}\) (\({\bf v}\) is the velocity).

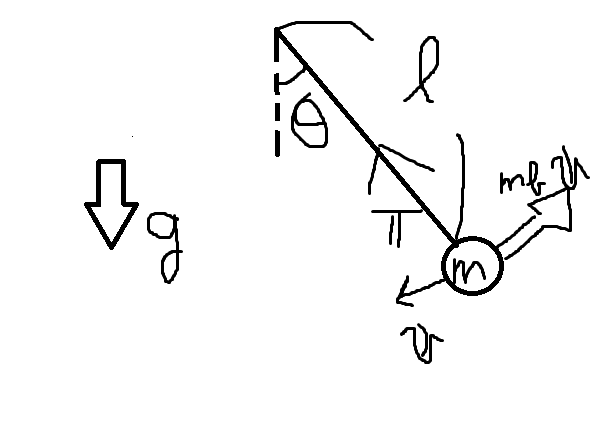
The equation of motion is

\(\)\begin{eqnarray} m\ddot{{\bf r}} = m{\bf g}-mb{\bf v}+{\bf T} \end{eqnarray}\)

with \({\bf r}\) the position vector.

Energy dissipation by air resistance

To derive the energy equation, taking the inner product of the equation of motion and \(\dot{\bf r}\),

\(\begin{eqnarray} m\ddot{{\bf r}}\cdot\dot{\bf r} = m{\bf g}\cdot\dot{\bf r}-mb{\bf v}\cdot\dot{\bf r}+{\bf T}\cdot\dot{\bf r} \end{eqnarray}\)

velocity and tension vectors are orthogonal.

The motion of a pendulum is part of a circular motion, the velocity vector and the tension vector are orthogonal as the above figure shows.
That is, \({\bf T}\cdot\dot{\bf r} = 0\).
Also, from

\(\begin{eqnarray} \frac{{\rm d}}{{\rm d}t}\frac{1}{2}m\dot{\bf r}^2 &=& m\ddot{{\bf r}}\cdot\dot{\bf r} \\ \frac{{\rm d}}{{\rm d}t}m{\bf g}\cdot{\bf r} &=& m{\bf g}\cdot\dot{\bf r} \end{eqnarray}\)

we get

\(\begin{eqnarray} \frac{{\rm d}}{{\rm d}t}\left(\frac{1}{2}m{\bf v}^{2}-m{\bf g}\cdot{\bf r}\right) = -mb{\bf v}^{2}. \end{eqnarray}\)

The left hand side represents the time derivative of the mechanical energy, so this can be seen as the equation for energy dissipation.

Putting \(\tau\) as the stopping time of the pendulum,

\(\begin{eqnarray} \left|\frac{1}{2}m{\bf v}^{2}-m{\bf g}\cdot{\bf r}\right|_{t = 0} = -\int_{0}^{\tau}mb{\bf v}^{2}{\rm d}t. \end{eqnarray}\)

If we set the initial angle of the pendulum \(\theta_{0}\),

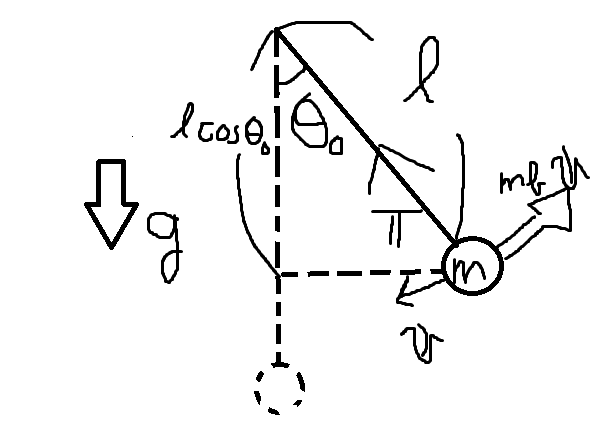
\(\begin{eqnarray} mgl\left(1-\cos\theta_{0}\right) = -\int_{0}^{\tau}mb{\bf v}^{2}{\rm d}t \end{eqnarray}\)

Summary

Now, that’s all what I wanted to write.

This time, I introduced a way to think about a pendulum with air resistance.

Thank you for reading and please spread this blog if you like.

If you have any comment, please let me know from the e-mail address below or the CONTACT on the menu bar.
tsunetthi(at)gmail.com
Please change (at) to @.

Or you can also contact me via twitter (@warotan3)