Let’s solve Lotka-Volterra equations!

Lotka-Volterra equations
Let’s solve in a numerical way
Disruption of ecosystem
Summary

Lotka-Volterra equations

The Lotka-Volterra equations is defined as

\(\begin{eqnarray}\frac{{\rm d}x}{{\rm d}t} &=& \alpha x-\beta xy \\ \frac{{\rm d}y}{{\rm d}t} &=& \gamma xy-\eta y \end{eqnarray}\)

\(\alpha,\,\beta,\,\gamma,\,\eta\) are parameters.

The equations model the predator-prey relationships.
Here, to understand easily, let us think of the predator as lions and the prey as zebras.
\(x\) represents the number of zebras and \(y\) is lions.

\(\begin{eqnarray} x &\rightarrow& The number of zebras\\ y &\rightarrow& The number of lions \end{eqnarray}\)

Let us consider the first equation

\(\begin{equation}\frac{{\rm d}x}{{\rm d}t} = \alpha x-\beta xy. \end{equation}\)

The left hand side \(\frac{{\rm d}x}{{\rm d}t}\) represents how much the population of zebras changes in a unit of time.
The first term on the right hand side \(\alpha x\) means that the population grows in proportion to the number of them, in other words, the more zebras there are, the easier they increase.
The second term \(\beta xy\) shows the decrease by lions. The negative sign represents decreasing and the more lions there are, the more zebras will be eaten.
Also, the more zebras, lions can eat them more easily, leading to the decrease of zebras.

Like this, the LV equations are differential equations that express the state of weak and strong competition in the natural world.
The meaning of the second equation is left for you.
Please think about it.

Let’s solve in a numerical way

The LV equations cannot be solved analytically, so let us solve in a numerical way as always.
The implementation is by C.

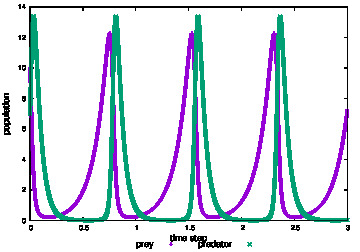
うまく食物連鎖が回っている — Grean points are lions (predators) and
purple ones are zebras (preys)

We did it!

The parameters are \(\alpha = 8.0,\,\beta = 4.0,\, \gamma = 6.0,\,\eta = 18.0\).

The green points are lions (predators) and the purple ones are zebras (preys).

At first, the number of zebras decrease and lions increase.
However, when the decrease of zebras comes to a certain level, lions also decrease.
Decrement of lions grows the number of zebras gradually and they can eat them again.
The solution shows a periodically behavior like this.

Disruption of ecosystem

If you change the parameters, you can also collapse the ecosystem and drive it to extinction, ruthless.

The population change with \(\alpha < 0\)

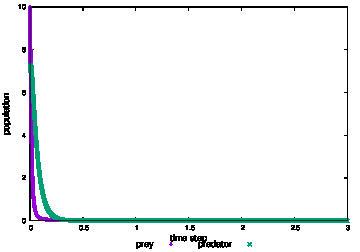
\(\alpha < 0\) is equivalent to introducing the decrease of zebras by some external factors into the equation (for example, overhunting by human).
If we add a new term \(\zeta x\) that means the external factors

\(\begin{eqnarray} \frac{{\rm d}x}{{\rm d}t} &=& \alpha x-\beta xy-\zeta x \\ &=& \left(\alpha-\zeta\right)x-\beta xy \end{eqnarray}\)

then we can give the model an explanation that if the index of the external factor \(\zeta\) is greater than the index of fertility of zebras \(\alpha\), the coefficient of the first term on the right hand side becomes negative and drive them to extinction.

Summary

Now, that’s all what I wanted to write.

This time, I tried solving the Lotka-Volterra equations.

Thank you for reading and please spread this blog if you like.

If you have any comment, please let me know from the e-mail address below or the CONTACT on the menu bar.
tsunetthi(at)gmail.com
Please change (at) to @.

Or you can also contact me via twitter (@warotan3)