みんにちは!わろたんです。
今回は高校物理でも習う、エネルギー保存のお話とそれを使って具体的な問題を解いてみたいと思います1。
何かと難しそうで敬遠されがちな物理ですが、生物や化学と比べて覚えることはめちゃ少ないと思います。
有機・無機化学とか地獄でしょ、あれ。。。
以下のような流れで説明していきます。
また、高校物理に関する記事は以下にまとめてあります。
→「高校物理」一覧
他の記事も読んでみて下さい!
エネルギーって何…?
エネルギーという言葉、よく聞きますね。
例えば電気エネルギー。
最近では電気自動車など、電気を動力源として走る車も出てきています。
また、エアコンやテレビなども電気を動力源として動いています。
他にも、エナジードリンクという飲み物もあります。
あれは、身体を動かす活力を生み出すとかそういう意味ですね。
このようにエネルギーとは
なんですね。
つまり、エネルギーが大きいというのは
何かしら物体を動かしたり、変形させたりしやすい
ということを意味しています。
力学的エネルギーって何…?
そんなエネルギーの中でも物理で重要なもののひとつに力学的エネルギーがあります。
力学的エネルギーには2つ種類があります。
運動する物体が持つ「運動エネルギー」と
物体がそこにあることによって物体が持つ「位置エネルギー」です。
運動エネルギー
例えば、時速20 km で走っているトラックと時速60 km で走っているトラックがあるとします。
この2台のトラックがそれぞれ壁に衝突したとします。
悲惨なことになるのは、どちらでしょうか。
時速 60km のトラックの方が衝突したときの被害が大きくなります。
当たり前ですね。
これを先ほどの言葉で言えば、
時速 60km のトラックの方が運動エネルギーが大きいので
トラックの車体とか乗っている人間とかの形を動かし、変形させる量が大きい
ということになります。
位置エネルギー
例えば、あなたはリンゴを2個持っているとします。
そのリンゴを2つの高さから落とすとします。
一つは、そうですねぇ。
その場でパッと落としてみますか。
手に持ったリンゴを自分の顔の横くらいから、勢いをつけずパッと手を放して落としてみます2。
結果は、まぁそんな大した傷などはつかず、早めに食べれば黒くなったりもせずおいしくいただけます。
もう一つは、例えばビルの屋上から落としてみますか。(絶対にやらないでください。)
リンゴはぐちゃぐちゃですね。残念です。
このように高さが違うと、リンゴの損傷具合も違ってきます。
これも先ほどの言葉で言えば、
高いところにあるリンゴの方が位置エネルギーが大きいので
リンゴの変形も大きい
ということが言えそうです。
繰り返しになりますが、このような2種類のエネルギーを力学的エネルギーと呼んでいます。
力学的エネルギーの保存とは…?
力学的エネルギーが保存するというのは、
ということです。(は?)
例えば振り子を考えてみます。空気抵抗とか摩擦とか何とかいうのは考えません。(空気抵抗等を考えると、力学的エネルギーは保存しません。)
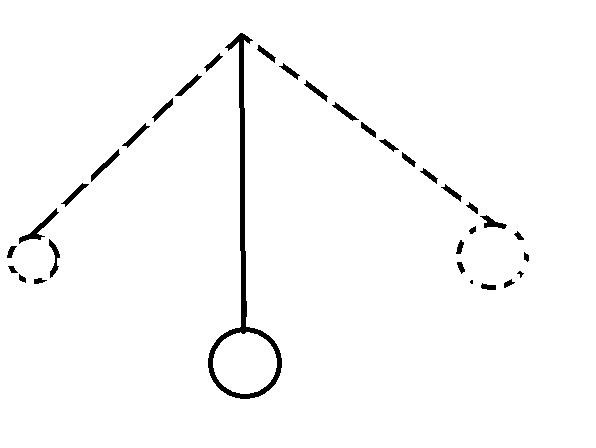
空気抵抗等を考えていないので、点線の位置に振り子をセットして手を放すと反対側で同じ高さまで上がって止まります。
その後またさらに反対側まで行って、同じ高さで止まります。
そしてこれは永遠に続きます3。
ではどの瞬間を切り取っても同じ値というのはどうしてわかるのでしょう。
実際、非常に中途半端な状態4というのは分かりづらいので
図の真ん中の、振り子が最下点にきたところを考えてみましょう。
いままでは振り子は一個だったのですが、ここでもう一個加えてみましょう。
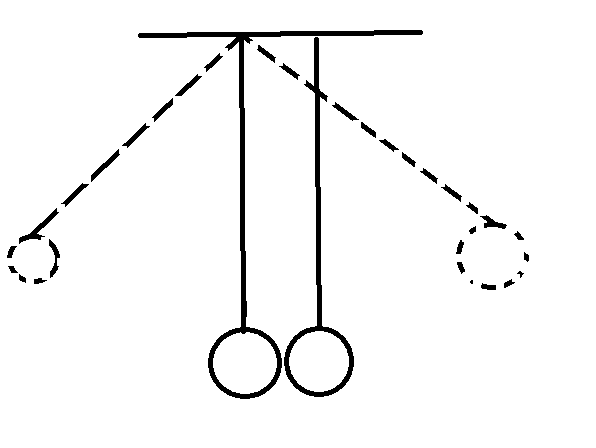
今まであった振り子のすぐ隣に新たに振り子を一個つるし、一方の振り子をある高さまで持ってきて(A)手を放します。
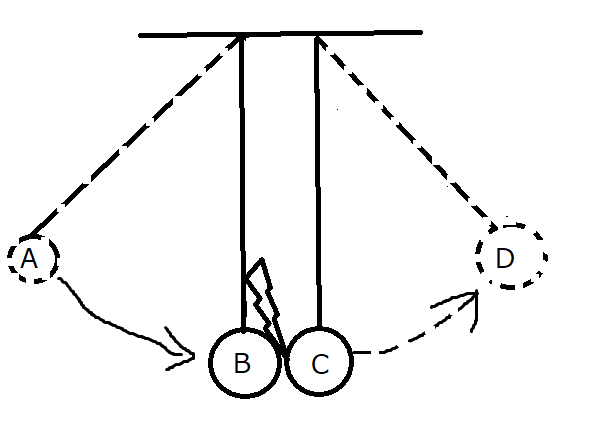
すると、衝突された振り子はもともと持ち上げた振り子と同じ高さまで上がります。
すなわち、図のAの位置にある振り子のもっていたエネルギーはBの位置に来ても同じ値で、それがもう一方の振り子Cに伝わってDの位置にまで上がってきたという理解ができます。
これで、どの瞬間を切り取っても同じ値ということの意味は分かっていただけたと思います。
ここで一つ注意しなければならないことがあります。
私はこの章の最初の方で、
と書きました。今の説明では、漠然とエネルギーが同じ値になっていることは理解できると思いますが、「運動エネルギーと位置エネルギーを足したものが」という説明にはなっていません。
なので、もう少し丁寧に説明していく必要があります。
実はよく考えると、振り子がAの状態で持っているエネルギーとBの状態で持っているエネルギーは違うものです。
何しろ、運動の状態が違います。Aは静止しているのに対して、Bでは動いています。
つまり、Aでは運動エネルギーがないのにBでは運動エネルギーがあります。
なので、先ほど同じ値と言ったのは実は別々のエネルギーに対して、それぞれ同じ値だということだったんですね。
だから、個々のエネルギー単体で見ると保存していないけれども、力学的エネルギーという全体で見ると保存している、つまり
ということになるんですね5。
まとめ
いかがだったでしょうか。
今回は高校物理の力学の基礎的な部分を解説してみました。
次回は今回の内容を基に、ちょっとした問題を解いてみたいと思います。
他にも色々と高校物理に関する記事を書いています。参考にしてください!
→「高校物理」一覧
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。