高校物理のお話～運動量保存則 (実践編)すべり台をころがる玉～

みんにちは！わろたんです。

今回は
高校物理のお話～運動量保存則 (基礎編)～
の知識を使って具体的な問題を解いていく、実践編です。

以前お話した問題をやっと解くことができます！

以下のような流れで説明していきます。

運動量保存則のおさらい
具体的な問題を解いていくぅ！
(1) 固定されたすべり台を転がった玉
(2) 台を固定していたストッパーを外すとどうなる…?
まとめ

また、高校物理に関する記事はこちらにまとめてあります。
他の記事も読んでみて下さい！

運動量保存則のおさらい

前回の結論を軽くおさらいしておきます。
運動量\(\vec{p}\)というのは、物体の止めにくさを表す物理量で

\(\begin{eqnarray} \vec{p}=m\vec{v} \end{eqnarray}\)

というふうに定義されるのでした。\(m\)は質量で\(\vec{v}\)は速度です。

また、運動量の変化量\({\rm d}\vec{p}\)というのは力積というものと関係していて

\(\begin{eqnarray} {\rm d}\vec{p} = \vec{F}{\rm d}t \end{eqnarray}\)

なる関係がありました。
つまり力をかけなければ運動量は変化しないということでした。
覚えてましたかな?

具体的な問題を解いていくぅ！

(1) 固定されたすべり台を転がった玉

質量\(M\)、高さ\(h\)の固定されたすべり台にセットされた質量\(m\)の質点Aがあります。

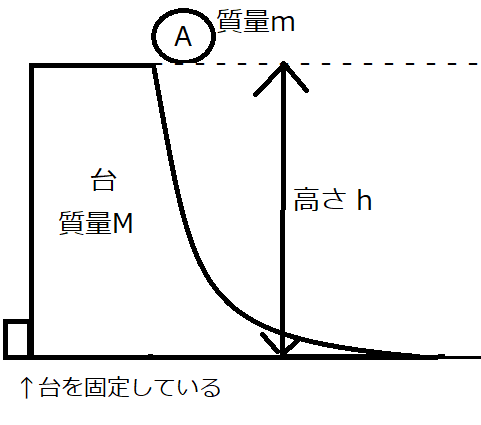
このとき、Aをすべり台からすべらしたとき最下点でのAの速さはいかほどでしょうか。
摩擦や空気抵抗は考えません¹。

エネルギー保存を考えてみましょう。
摩擦等を考えなければ、力学的エネルギーは運動のどの瞬間をとっても保存するのでした。
考える状態として、初期状態と最下点の状態をとってみようと思います。

初期状態では運動している物体はありません。
Aは手に持たれて、高さ\(h\)の位置に静止しています。
なので初期状態の運動エネルギーは0です。

一方、位置エネルギーの方はどうでしょう。
すべり台の最下点を基準にすると、Aが重力の位置エネルギー

\(\begin{eqnarray} U_{A} = mgh \end{eqnarray}\)

を持っています。
従って、初期状態の力学的エネルギーは

\(\begin{eqnarray} E_{{\rm init}} = mgh \end{eqnarray}\)

となります。

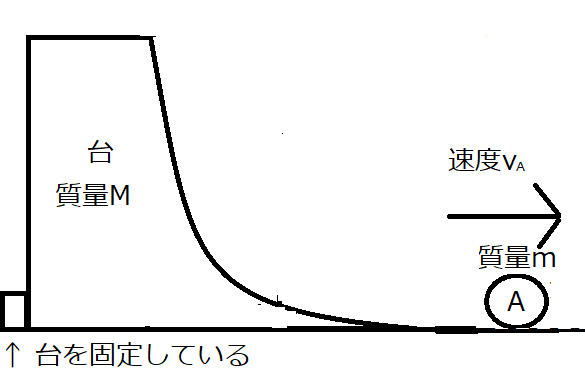
手を放し、最下点で物体Aは速度\(v_{A}\)で進んだとします。

このとき、運動エネルギーは

\(\begin{eqnarray} K = \frac{1}{2}mv_{A}^{2} \end{eqnarray}\)

また、全ての物体が基準面上にあるので位置エネルギーは0です。
よって最下点の力学的エネルギーは

\(\begin{eqnarray} E_{{\rm after}} = \frac{1}{2}mv_{A}^{2} \end{eqnarray}\)

力学的エネルギー保存則より

\(\begin{eqnarray} E_{{\rm init}} &=& E_{{\rm after}} \\ mgh &=& \frac{1}{2}mv_{A}^{2} \end{eqnarray}\)

よって

\(\begin{equation} v_{A}=\sqrt{2gh} \end{equation}\)

実はこの問題はエネルギー保存だけで解ける問題だったのです。
しかし、次のような問題はどうでしょうか。

(2) 台を固定していたストッパーを外すとどうなる…?

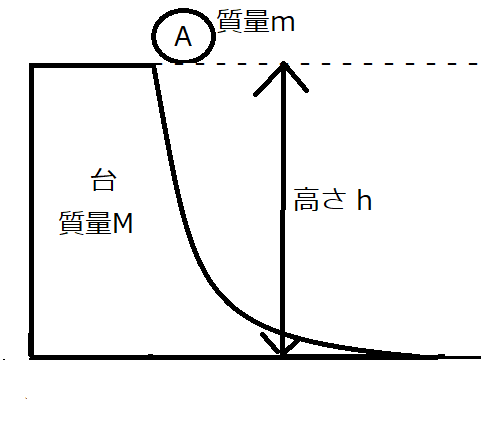
今度は台を固定していたものを外して、台が水平方向に自由に動ける場合を考えてみましょう。
この問題を考えることによって、エネルギー保存がどういうことかの理解が進むと思います。

エネルギー保存を考えるにあたって、力学的エネルギーを考えていきます。
まずは上図の状態を考えていきましょう。

運動している物体はないので運動エネルギーは0です。
位置エネルギーは物体Aの持つ重力による位置エネルギーがあって、
結局力学的エネルギーは

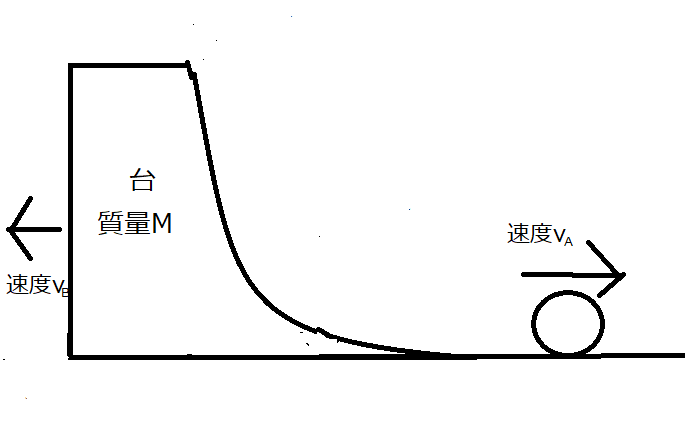
\(\begin{equation} E_{{\rm init}} = mgh \end{equation}\)

状況が違うのは、玉が転がって速度\(v_{A}\)を持ったときです。
何しろ、台が固定されていないので台も速度\(v_{B}\)で動いてしまいます。
この状態での力学的エネルギーは²

\(\begin{equation} E_{{\rm after}} = \frac{1}{2}mv_{A}^{2}+\frac{1}{2}Mv_{B}^{2} \end{equation}\)

この場合、どういう風に考えていくかというと

最初に球Aが持っていた位置エネルギーが
台の運動エネルギーと球の運動エネルギーに分散した

と考えるのです。
つまり、力学的エネルギー保存則は以下のようになります;

\(\begin{eqnarray} E_{{\rm init}} &=& E_{{\rm after}} \\ mgh &=& \frac{1}{2}mv_{A}^{2}+\frac{1}{2}Mv_{B}^{2} \end{eqnarray}\)

次に運動量保存則を考えます。

初期状態では何も動いていないので全体として運動量は0です。
Aが最下点にくるとAは速度\(\vec{v}_{A}\)、台は速度\(\vec{v}_{B}\)を持っているので運動量保存則は³

\(\begin{eqnarray} 0 = m\vec{v}_{A}+M\vec{v}_{B} \end{eqnarray}\)

よってエネルギー保存則と合わせて

\(\begin{eqnarray} \left\{ \begin{array}{} mgh &=& \frac{1}{2}mv_{A}^{2}+\frac{1}{2}Mv_{B}^{2} \\ 0 &=& mv_{A}+Mv_{B} \end{array} \right. \end{eqnarray}\)

第2式より⁴

\(\begin{equation} v_{A}=-\frac{M}{m}v_{B} \end{equation}\)

第1式に代入して

\(\begin{eqnarray} mgh &=& \frac{1}{2}m\left(-\frac{M}{m}v_{B}\right)^{2}+\frac{1}{2}Mv_{B}^{2} \\ &=& \left(\frac{M^{2}}{2m}+\frac{M}{2}\right)v_{B}^{2} \\ &=& \frac{M}{2}\left(1+\frac{M}{m}\right)v_{B}^{2} \end{eqnarray}\)

よって

\(\begin{eqnarray} \frac{2m}{M}\frac{1}{1+\frac{M}{m}}gh = v_{B}^{2} \end{eqnarray}\)

従って

\(\begin{eqnarray} v_{B} &=& \sqrt{2gh\frac{m^{2}}{M\left(m+M\right)}} \\ &=& m\sqrt{2gh\frac{1}{M\left(m+M\right)}} \end{eqnarray}\)

\(v_{A}\)は

\(\begin{equation} v_{A} = -M\sqrt{2gh\frac{1}{M\left(m+M\right)}} \end{equation}\)

まとめ

いかがだったでしょうか。

今回は運動量保存則を使う問題を解きつつ、

エネルギーが保存するというのはどういうことなのか

の理解を深める問題を解いてみました。

私自身は高校の時に似たような問題を解いて、非常に感動した覚えがあります。
エネルギー保存は、物理学科⁵に進むと非常に長い付き合いになりますので
ここでざっくりとイメージをつかんでおくことは大事だと思ったので、この記事を書きました。

他にも色々と高校物理に関する記事を書いていますので参考にしてください！

もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。

tsunetthi(at)gmail.com

(at)の部分を@に変えてメールをお送りください。

これを入れると、大学以上でやる話になります。
実はエネルギーは個別に求めて足しておくと、全体のエネルギーを表すことができます。
実は運動量はエネルギーと違ってベクトル量なので座標系が大事です。今回は重心系という座標系で考えていることになっています。
この式より、球と台は互いに反対方向に動くということが分かります
他の学科はよく知りませんが、色々なところでお目にかかるのは確かです。