高校物理のお話～運動量保存則 (基礎編)～

みんにちは！わろたんです。

前回、エネルギー保存のお話をしましたが、
力学でエネルギー保存と双璧をなすもう一つの保存則、運動量保存則についてです。
関連記事: 高校物理のお話～エネルギー保存 (実践編)～

以下のような流れで説明していきます。

運動量って何…?
運動量保存則
まとめ

また、高校物理に関する記事は以下にまとめてあります。
→「高校物理」一覧
他の記事も読んでみて下さい！

運動量って何…?

運動量\(\vec{p}\)というのは、数式的には

\(\begin{eqnarray} \vec{p}=m\vec{v} \end{eqnarray}\)

と書きます。\(m\)というのは質量で、\(\vec{v}\)は速度です。
つまり、物体の質量と速度の積のことを運動量と呼んでいるんですね。(HA?)

例えば、時速20 km で進む4tトラックと時速 40 km で走る自転車があったとしましょう。なかなかのスピードで走る自転車ですね。

さて、もしこいつらを止めようとした場合、どちらの方が止めるのが大変でしょうか。
時速 20 km のトラックは遅いですがなかなか重量があります。
一方、時速 40km の自転車は速いですが軽いです。

これを先ほどの運動量の式を基に考えてみましょう。
まず、4tトラックの方は質量は大体400 kg くらいで、速さは秒速に直すと約5.6 m/s くらいです。なので

\(\begin{eqnarray} p_{{\rm track}} &\simeq& 400\times 5.6 \\ &=& 2400 \,\,{\rm kg\,m/s} \end{eqnarray}\)

一方自転車の方は、質量は大体1 kg くらいで、速さは約11 m/s くらいですので、

\(\begin{eqnarray} p_{{\rm track}} &\simeq& 1\times 11 \\ &=& 11 \,\,{\rm kg\,m/s} \end{eqnarray}\)

4t トラックの方が200倍くらい止めるのが大変ということになります。
この場合は速さというよりは、4t トラックが非常に重いので止めるのが大変という結果が得られました。
運動量のイメージは大体つかめましたかね。

運動量保存則

先ほど止めるのが大変と言いましたが、それは具体的にどういうことでしょうか。
実は、止めるのに必要なある一定の力をかけ続ける時間が長いということを「大変」と言っていたと理解できるのです。

運動している物体を止めるということは、その物体の速度を0にすることですが
それはすなわち、運動量を0にするということです;

\(\begin{eqnarray} \vec{p}=m\vec{v} \end{eqnarray}\)

みなさん、想像してみてください。
みなさんに向かってショッピングカートが速度\(\vec{v}\)で突進してきています。
そのショッピングカートを止めようとしたら、みなさんどうしますか。

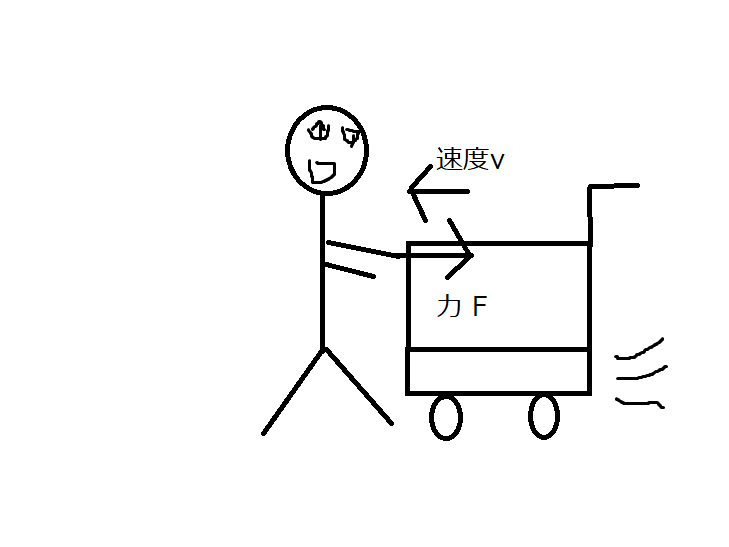
きっと、カートの動きと逆向きに力を加えて止めようとするのではないでしょうか。

力Fをかけて止めます

仮に、ある一定の力\(F\)しか出せないとしてみると
止めにくい物体を止めるためには、より長く力をかけ続けなければならない
ということになります。
または、非常に短い時間で止めたかったら、非常に大きな力が必要になるというのも何となくイメージがつくと思います。
つまり、一方を大きくすると他方は小さくても良いという関係になっているのですね。

こういったものをよく表す物理量として、力積という考え方があります。
つまり、力の大きさと力のかかる時間をひとまとめにして積として考えようというものです。

実は、この力積と運動量の変化量というのは関係がありまして

\(\begin{eqnarray} {\rm d}\vec{p} = \vec{F}{\rm d}t \end{eqnarray}\)

と書かれます。\({\rm d}\vec{p}\)は運動量の変化量を表し、
右辺の\(\vec{F}{\rm d}t\)というのが力積というのものです。

この式からわかるように、運動量が保存する、すなわち運動量の変化量が0であるためには力積が0であれば良いということになります。
平たく言えば、何も力をかけなければ運動量は変化しないということです。
何も力をかけなければ、運動の向きや速度は変化しませんもんね。
分かりやすく言えば、そういうことを言っているのです。