みなさん、こんにちは!わろたんです。
今回は\(\phi^4\) kinkをアニールしてみたという記事において使った数値微分・数値積分法の精度について記事にしてみたいと思います。
公式の具体的な導出も書いておくので、勉強中の方でちょっと理解に詰まった方などは参考にしてみて下さい!!
今回の記事は以下のような流れになっています。
ご自分の興味に合わせて読んでください!!
数値微分
まずは微分の復習からだぬ!
まずは微分の定義を復習しましょう!簡単のために1変数の微分を考えます。
まず、関数\(f\left(x\right)\)の微分というのは数学的には
\(\displaystyle \begin{equation}\frac{{\rm d} f}{{\rm d} x}=\lim_{h\to 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}\end{equation}\)
というふうに定義されていますね。これは、前進差分による微分と呼ばれてるものです。
コンピュータ上で微分する!
しかしながらコンピュータ上の計算では、極限\(\displaystyle
\lim_{h\to 0}\)というのがとれず、有限の大きさで常に止まってしまうので、解析的な微分からはズレてしまいます。よくあるTaylor展開から
\(\begin{equation}f\left(x+h\right)=f\left(x\right)+f’\left(x\right)h+O\left(h^2\right)\end{equation}\)
より
\(\begin{equation}f’\left(x\right)=\frac{f\left(x+h\right)-f\left(x\right)}{h}+O\left(h\right)\end{equation}\)
このように、単純な離散化では\(O\left(h\right)\)程度の精度しか出ません。
近似の精度を上げる
そこで近似の精度を上げるために、次のようなことを考えます。
まず、上のTaylor展開で\(h\to -h\)ということをすると
\(\begin{equation}f\left(x-h\right)=f\left(x\right)-f’\left(x\right)h+\frac{1}{2!}f”\left(x\right)h^2+O\left(h^3\right)\end{equation}\)
一方、この変換を行う前の展開の式は
\(\begin{equation}f\left(x+h\right)=f\left(x\right)+f’\left(x\right)h+\frac{1}{2!}f”\left(x\right)h^2+O\left(h^3\right)\end{equation}\)
この2式の引き算から
\(\begin{equation}f\left(x+h\right)-f\left(x-h\right)=2f’\left(x\right)h+O\left(h^3\right)\end{equation}\)
すなわち
\(\begin{equation}f’\left(x\right)=\frac{f\left(x+h\right)-f\left(x-h\right)}{2h}+O\left(h^2\right)\end{equation}\)
この公式による微分を中心差分による微分といいます。注目すべき点は、先ほどの前進差分による数値微分が
\(O\left(h\right)\)程度の精度しかなかったのに対し、中心差分による数値微分は
\(O\left(h^2\right)\)の精度をもつということです。
実際にやってみた…(^_^)/
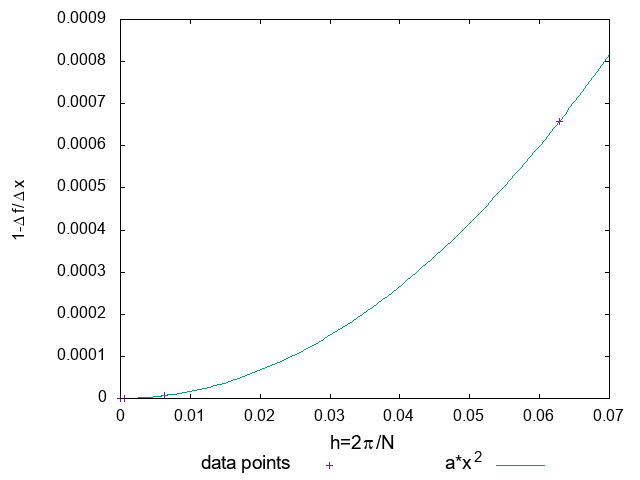
以下は\(f\left(x\right)=\sin\left(x\right)\)について、\(x=0\)の点の数値微分による微係数\(\Delta f/\Delta x\)を分点数\(N\)を変えてプロットしたものです。きちんと\(O\left(h^2\right)\)の振る舞いが見えていることが確認できると思います。
 中心差分による数値微分の精度確認
中心差分による数値微分の精度確認
刻み幅\(h=2\pi/N,\: N\)は分点数
に対して、\(O\left(h^2\right)\)の振る舞いをしている
もっと精度を上げたい
実は、後でSimpson公式による数値積分を実行した結果を示しますが、そのときに思ったほど精度が出なくておかしいなぁと思ったら、数値微分の精度が足りなかったことが原因だと判明したので、精度を上げて\(O\left(h^4\right)\)の微分公式も使ってみました。ただし一部、\(n\)階微分を\(f^{\left(n\right)}\)のように書きました。
導出は中心差分による微分のときとほとんど同じようなことをやればよくて、
\(\begin{equation}f\left(x\pm h\right)=f\left(x\right)\pm f^{\left(1\right)}\left(x\right)h+\frac{1}{2!}f^{\left(2\right)}h^2\pm\frac{1}{3!}f^{\left(3\right)}h^3+\frac{1}{4!}f^{\left(4\right)}h^4+O\left(h^5\right)\end{equation}\)
それから\(h\to 2h\)として
\(\begin{equation}f\left(x\pm 2h\right)=f\left(x\right)\pm f^{\left(1\right)}2h+\frac{1}{2!}f^{\left(2\right)}\left(2h\right)^2\pm\frac{1}{3!}f^{\left(3\right)}\left(2h\right)^3+\frac{1}{4!}f^{\left(4\right)}\left(2h\right)^4+O\left(h^5\right)\end{equation}\)
これらより
\(\begin{align}f\left(x+h\right)-f\left(x-h\right)&= 2f^{\left(1\right)}h+\frac{1}{3}f^{\left(3\right)}h^3+O\left(h^5\right) \\
f\left(x+2h\right)-f\left(x-2h\right)&= 4f^{\left(1\right)}h+\frac{8}{3}f^{\left(3\right)}h^3+O\left(h^5\right)
\end{align}\)
よって
\(\begin{equation}8\left[f\left(x+h\right)-f\left(x-h\right)\right]-\left[f\left(x+2h\right)-f\left(x-2h\right)\right]+O\left(h^5\right)=12f’\left(x\right)h\end{equation}\)
以上より
\(\begin{equation}f’\left(x\right)=\frac{1}{12h}\{8\left[f\left(x+h\right)-f\left(x-h\right)\right]-\left[f\left(x+2h\right)-f\left(x-2h\right)\right]\}+O\left(h^4\right)\end{equation}\)
めでたく\(O\left(h^4\right)\)の精度をもつ数値微分の公式が出来上がりました!やったね(^-^^)/
Simpson公式による数値積分
\(f\left(x\right)=\sin\left(x\right)\)の微分の2乗の半分\(\frac{1}{2}f’\left(x\right)^2=\frac{1}{2}\cos^2\left(x\right)\)に対して\(x\in\left[0,2\pi\right]\)で積分しました。まず、解析的には
\(\begin{align}I&\equiv \frac{1}{2}\int_{0}^{2\pi}\left(f’\left(x\right)\right)^2 \\
&= \frac{1}{2}\int_{0}^{2\pi}\cos^2\left(x\right) \\
&= \frac{1}{2}\int_{0}^{2\pi}\frac{1+\cos\left(2x\right)}{2}{\rm d} x\\
&= \frac{1}{2}\frac{1}{2}2\pi \\
&= \frac{\pi}{2}
\end{align}\)
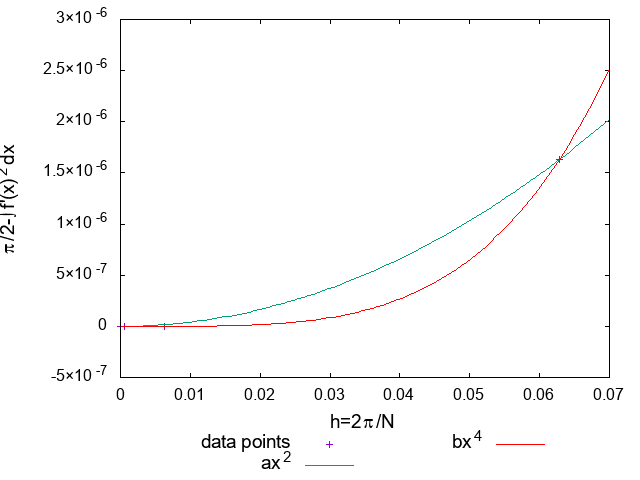
次に数値積分をした結果を載せます。
 分点数\(N=10^2,10^3,10^4,10^5,10^6,10^7\)に対して数値積分を行った。
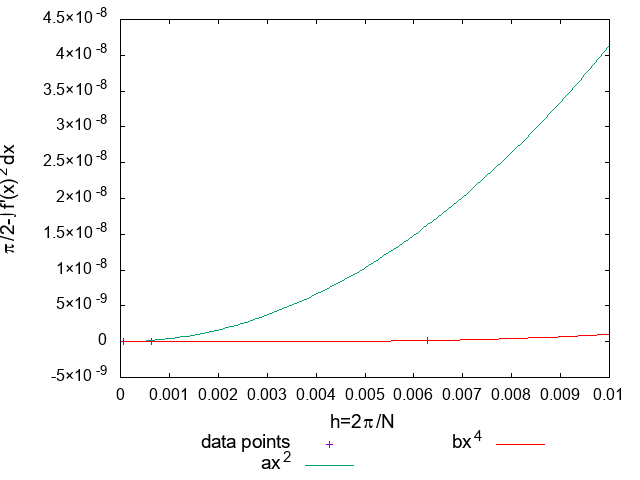
分点数\(N=10^2,10^3,10^4,10^5,10^6,10^7\)に対して数値積分を行った。 \(h\simeq 0\)近傍
\(h\simeq 0\)近傍以上より、\(O\left(h^4\right)\)っぽい振る舞いが見えました。負の値が出ていますが、大きさとしては\(10^{-15}\)程度なので数値誤差だと考えられます。
おまけ
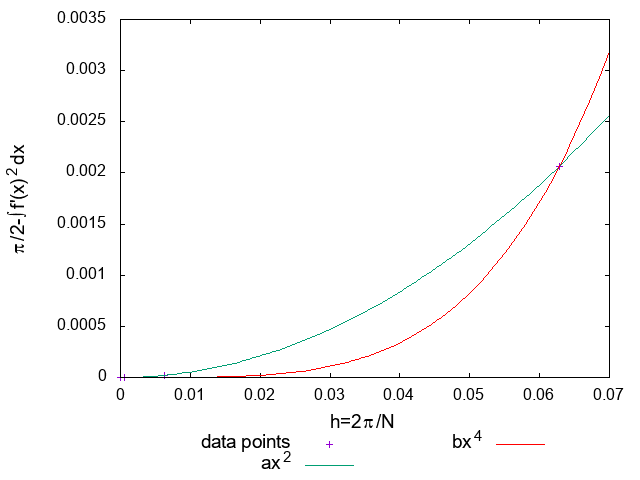
微分を\(O\left(h^2\right)\)精度のままやると次のようになりました。

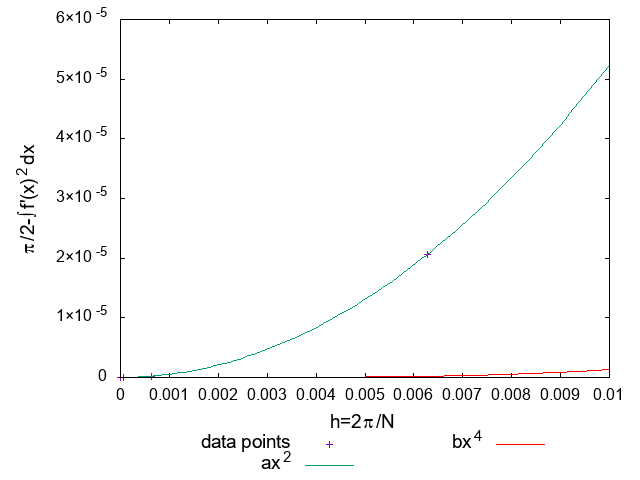
分点数\(N=10^2,10^3,10^4,10^5,10^6,10^7\)に対して数値積分を行った。 \(h\simeq 0\)近傍
\(h\simeq 0\)近傍以上のようなことから、このグラフにおいて精度が\(O\left(h^2\right)\)のように見えているのは、数値微分の精度が効いていたことがわかります。
まとめ
いかがだったでしょうか。
今回は\(\phi^4\) kinkをアニールしてみたで使った数値微分・数値積分の紹介をしました。
勉強中のみなさんのお力になれれば幸いです!
最後まで読んでいただきありがとうございました!!
他にも色々とシミュレーションに関する記事を書いています。ぜひ読んでみて下さい!
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。