競プロの問題を解いていると約数列挙が必要な場合があります。
今回は約数列挙のアルゴリズムについてお勉強したので忘れないうちにまとめて記憶の定着を図ろうと思います。
また、競プロ関連の記事は他にも書いています。今後必要なことを拡充していきたいと思いますので参考にしてみて下さい!
→「プログラミングコンテスト」一覧
そもそも約数って何だっけ?
数学において、整数N の約数(やくすう、英: divisor)とは、N を割り切る整数またはそれらの集合のことである。 (Wikipedia)1
例えば6の約数は1,2,3,6ですし、12の約数は1,2,3,4,6,12です。
やり方は色々ある
約数列挙のやり方は色々あります。
今回はその中でよく使いそうな2つくらい書いておこうと思います。
1. 単純に割りまくる
約数の定義から、ある整数\(n\)の約数を求めようとしたら
という方法があります。
本当に愚直にやると\(O\left(n\right)\)かかってしまいますが、以下のように\(O\left(\sqrt{n}\right)\)で済むことが分かります。
まず、約数の定義からある整数\(n\)の約数latex]a,b[/latex]は以下のように表すことができます。
この式から、もしある整数\(a\)が\(n\)の約数であった場合、\(n/a\)もまた約数であることが分かります。
従って\(a\)を1から順に試していって\(\sqrt{n}\)を超えたところで約数を発見した時、それはすでに\(n/a\)という約数として見つかっています。
このような対称性から試すべき約数は\(O\left(\sqrt{n}\right)\)であることが分かります。
実装例
上記を実装すると以下のようになると思います。
vector<long long> find_divisor(long long n){
vector<long long> divs;
for(long long a = 2; a * a < n; a++){
if(n % a == 0){
divs.push_back(a);
if(a*a != n) divs.push_back(n/a);
}
}
return divs;
}divsという配列に約数を突っ込んでいきます。
一つ注意点は\(n/a\)を忘れずに約数の配列に追加することです。
先ほどの説明の\(b = n/a\)に相当します。
これが必要なのは二つの約数が違うときだけなのでif文で分岐させています。
これにより\(O\left(\sqrt{n}\right)\)で約数列挙をすることができます。
2. 約数にマーキングする
上記とは別のアプローチとして約数にマーキングをして約数を全部列挙するという方法もあります。
まず、1~\(n\)までの表を作ります。
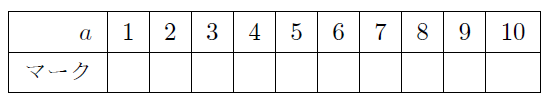
例えば\(n = 10\)の場合を考えます
最初に\(a = 1\)の場合を考えます。そして\(a\)の倍数のところにマークを付けていきます。

\(n = 10\)にマークがつきました。つまり、10は1の倍数、すなわち1は10の約数です。
次に\(a = 2\)の場合を考えます。同じように\(a\)の倍数のところにマークを付けていきます。

\(n = 10\)のところにマークがついたので\(a = 2\)も\(n\)の倍数であることが分かりました。
以降、3~\(n\)まで同様の操作をすると\(n\)の約数が全て列挙できることになります。
ちなみに\(a = 3\)は以下のような表になるので10の約数ではないことが分かります。

この方法だと各\(a\)でつけるマークの数は
となり、先ほどのやり方より少し遅いですが使いどころはあります。
今回は一つの整数の約数を考えていましたが、複数の整数の約数のリストを作りたい時などは\({\rm max}\, n_{i}\)を配列としてとっておいて後から上記操作をすることで、
各整数に対して\(O\left(\sqrt{n}\right)\)で計算する2よりも場合によっては高速に約数のリストを作ることができます。
実装例
上記を実装するとこんな感じになると思います。
vector<int> find_divisors_log(int n){
vector<int> ans;
for(int i = 2;i <= n; i++){
vector<bool> x(n+1,false);
for(int j = i;j <= n; j += i){
x[j] = true;
}
if(x[n]) ans.push_back(i);
}
return ans;
}まとめ
今回は約数列挙の方法についてよく使いそうなものをまとめてみました!
僕の理解だけでなく、これを読んだ方の理解の助けになれば幸いです。
関連記事: 実装例あり!最大公約数gcd・最小公倍数lcmを求める
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
サムネイル画像はpixabayさんからダウンロードさせていただきました!
ありがとうございます!



