Let’s use queue brilliantly!Breadth First Search with C++!

Hello, guys! It’s me! Warotan!
So…Who are you?→ABOUT MEJ

Japanese version.

For a given network, we sometimes need to know the minimum cost from a vertex to the all of them.
One of the methods used to efficiently solve such problem is BFS (Breadth First Search).

I write similar articles and will add contents, so please read more other articles.

What is BFS?

Breadth-first search (BFS) is an algorithm for searching a tree data structure for a node that satisfies a given property. (Wikipedia)

Let us think about surfing the net.
Each site has links with each other and constructs some networks.

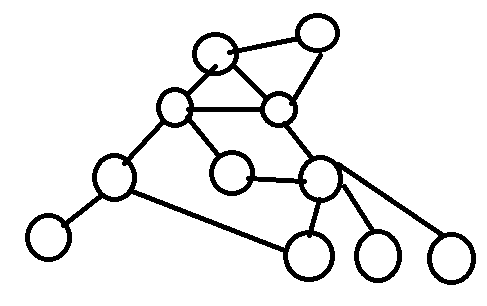
If you ask something to Google, you will get the list of related pages.
BFS is like you first open all of the results and see one by one.
On the other hand, you can also open one of the results and go deep by clicking the links on the site, which is called DFS (Depth First Search).
You can visit all of the sites with either way you want, but there is a different in that
BFS searches the broad set of the sites,
and DFS searches the links on the site you first access and go deeper and deeper into the links.

Searching the sites with the flag knowing that you already visited or not, you can see all of the sites with \(O\left(N+M\right)\) clicks because each site is visited only once at most.

Compatible data structures and transitions

BFS has a good match with the data structure called “Queue”.

A queue is a data structure in which the direction of data entry and exit is one-way.

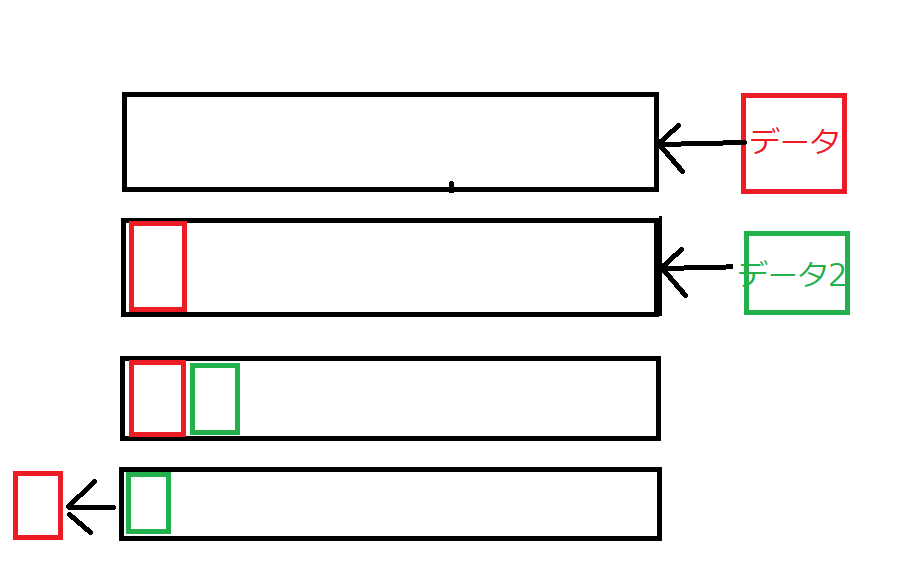
In this structure, we can’t extract the data2 before data1.

This matches with BFS algorithm.
Pushing the sites we visit into the queue one by one and extracting the head one to decide the direction, we can search all of the sites.

In the above image, the data transition is written like this;

[1] -> [] -> [3,4,2] -> [4,2] -> [4,2,5,6] -> [2,5,6] -> [2,5,6,7] -> [5,6,7] -> [6,7] -> [6,7,8,9] -> [7,8,9] -> [8,9] -> [8,9,10,11] -> [9,10,11] -> [10,11] -> [11] -> []

Implementation example

void bfs(vector<vector<int>> &Graph, vector<int> &dist){
  for(int i = 0;i<n;i++) dist[i] = -1;
  queue<int> q;

  dist[0]=0;
  q.push(0);
  while(!q.empty()){
    int v = q.front();q.pop();
    //if(dist[v]!=-1) continue;
    
    for(auto nv : Graph[v]){
      if(dist[nv]!=-1) continue;
      
      dist[nv]=dist[v]+1;
      q.push(nv);
    } 
  }
}

“Graph” has the network information and “dist” has the distance information.
Setting “dist” to -1, we can judge if the vertex is already visited or not.

This time starting from the vertex 0, setting dist[0] = 0 and pushing the vertex 0 into the queue.
After that, it repeats this until the queue is empty and saves the distances between vertices.
We can get the minimum distances between the vertex 0 and all others.

Summary

Now, that’s all what I wanted to write.

This time, I introduced BFS which is a popular searching method for a graph.

Thank you for reading and please spread this blog if you like.

If you have any comment, please let me know from the e-mail address below or the CONTACT on the menu bar.
tsunetthi(at)gmail.com
Please change (at) to @.

Or you can also contact me via twitter (@warotan3)