みんにちは!わろたんです。
今回はコンピュータの偉大なる力によって円周率をゴリ押しで求めちゃおうという企画です。
今回は以下のような流れで説明していきますので、いつものようにご自分の興味に合わせて読んでみて下さい!
考え方~目をつぶってダーツをする~
そもそもみなさん、円周率と聞いてどんなことを思い浮かべますか?
半径 \(r\) の円の円周が \(2\pi r\) なこと?
円の面積が \(\pi r^2\) なこと?
はたまた \(\left(\frac{1}{2}\right)!=\sqrt{\pi}\) でしょうか?
関連記事: ガンマ関数についてのお話~階乗の一般化~
今回は円の面積に注目しましょう。
円の面積は \(\pi r^2\) です。半径1の円を考えますと、その面積は \(\pi\) です。簡単ですね。
簡単に言うと、目をつぶってこの半径1の円に向かってでたらめにダーツを投げて、命中したものと外したものの比を取れば、それは円周率に収束していくだろうということです。
ダーツを一回投げて的に当たると1点、外すと0点というゲームを考えます。ダーツを一回投げて\(1/4\) 円に当たる確率は\(\pi/4\) なので、ダーツを投げた回数\(N\) 、当たった数を\(n\) とするとたくさん投げれば得点の期待値\(\frac{n}{N}\)は\(\pi/4\) に近づいていきます。なのでダーツをたくさん投げていけば\(\frac{4n}{N}\) は\(\pi\) に近づいていきます。
ダーツをやってみる
さて、この半径1の円に向かってダーツを投げて下さい。ただし、目をつぶって。周囲には十分気を付けて下さいね。
どのくらい投げればよいかというと、そうですねぇ。動画では2000回ほど投げています。お疲れさまでした。
やる気なくなったでしょ。
ですが、コンピュータでやれば一瞬です。1秒もかかりません。
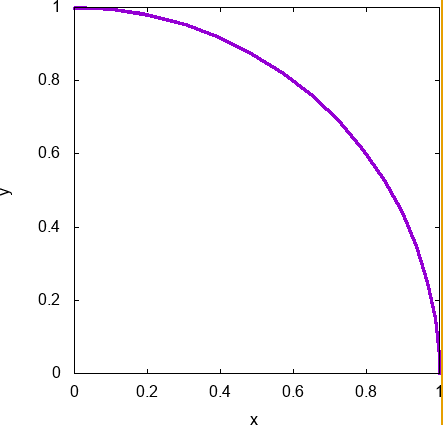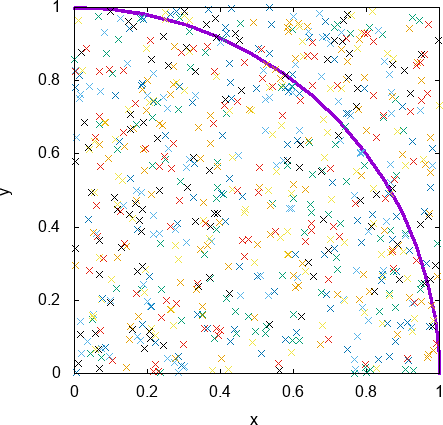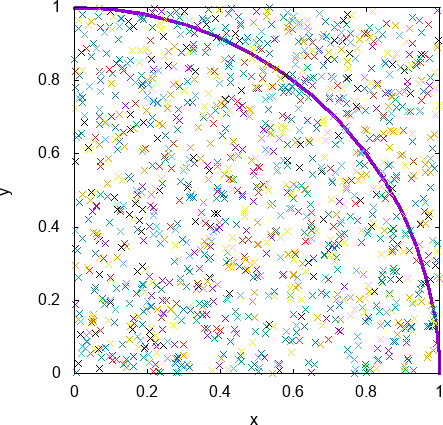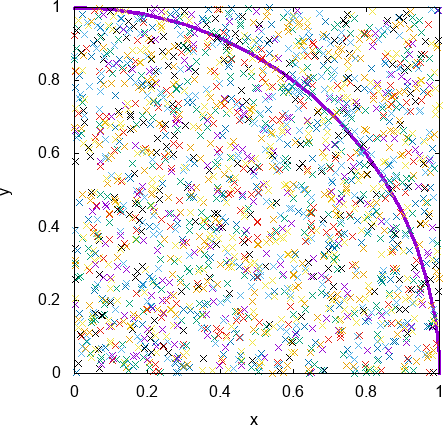
これは\(1/4\) 円に注目した動画です。
紫で描かれているのが的の端で、その内側に的があると思ってください。
これを見るとわかるように当然、的に見事命中したダーツと残念ながら外してしまったダーツがあることがわかります。でたらめに投げているのでしょうがありません。
では、ダーツを投げた数と当たった数の比を計算して円周率を求めてみましょう。
今回は\(\frac{\pi}{4}\) を求めてみます。定数倍しか違わないので、どちらを求めても一緒ですね。
下図は200回ダーツを投げるごとに的に当たった数とそれまで投げた数の比をとったもののプロットです。
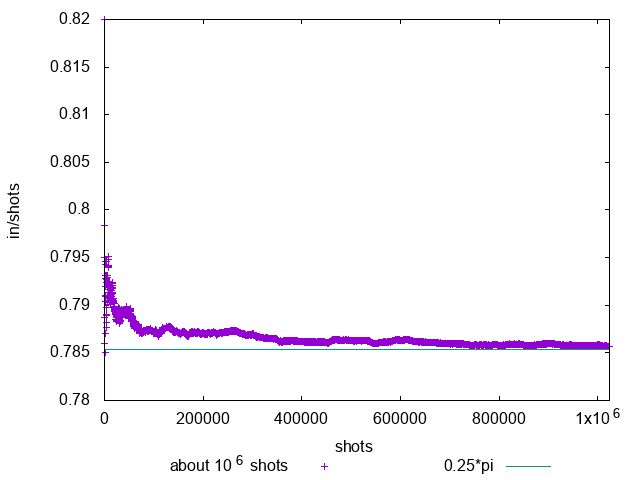
やってみて思いましたが、結構収束が遅いです。ですが、きちんと\(\frac{\pi}{4}\) に近づいていく様子がわかると思います。
コンピュータを使った数の暴力により、強引に円周率を求めることが出来ました。
まとめ
いかがだったでしょうか。
今回は円周率をコンピュータで計算してみました。
収束が遅いのは数学的に説明できるのですが、それはまたの機会としておきます。
最後まで読んでいただきありがとうございました!!
他にも色々とシミュレーション関連の記事を書いています。ぜひ読んでみて下さい!
→「シミュレーション」一覧
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。



