このページではφ^4 kinkをアニールしてみたという記事の中に出てくる計算の細かいところを詰めています。
日ごろのみなさんの勉強の中で、式変形につまったりしたら参考にしてみて下さい。
細かい計算について
ボゴモルニー方程式
\(\begin{equation}\frac{{\rm d}\phi}{{\rm d} x}=\sqrt{2\lambda}\left(m^2-\phi^2\right)\end{equation}\)
を考える。ここでは、解を知らないものとして求めていく。まず、\(\phi=m\zeta\)と置くと
\(\begin{equation}
m\frac{{\rm d}\zeta}{{\rm d} x}=m^2\sqrt{2\lambda}\left(1-\zeta^2\right)\end{equation}\)
m\frac{{\rm d}\zeta}{{\rm d} x}=m^2\sqrt{2\lambda}\left(1-\zeta^2\right)\end{equation}\)
よって
\(\begin{equation}\frac{{\rm d}\zeta}{{\rm d} x}=\sqrt{2\lambda m^2}\left(1-\zeta^2\right)\end{equation}\)
ゆえに
\(\begin{equation}\frac{{\rm d}\zeta}{1-\zeta^2}=\sqrt{2\lambda m^2}{\rm d} x\end{equation}\)
少し計算すると
\(\begin{align}\int\frac{{\rm d}\zeta}{1-\zeta^2}&= \int{\rm d}\zeta\left(\frac{1}{1-\zeta}+\frac{1}{1+\zeta}\right)\frac{1}{2} \\
&= \frac{1}{2}{\rm ln}\left|\frac{1+\zeta}{1-\zeta}\right|+{\rm const.} \\
&= \sqrt{2\lambda m^2}x+{\rm const.}
\end{align}\)
よって積分定数を\(\alpha\)と書くと
\(\begin{equation}\frac{1+\zeta}{1-\zeta}={\rm e}^{2\sqrt{2\lambda m^2}\left(x-\alpha\right)}\end{equation}\)
\(\begin{align}
\zeta&= \frac{{\rm e}^{2\sqrt{2\lambda m^2}\left(x-\alpha\right)}-1}{{\rm e}^{2\sqrt{2\lambda m^2}\left(x-\alpha\right)}-1} \\
&= {\rm tanh}\left(\sqrt{2\lambda m^2}\left(x-\alpha\right)\right)\end{align}\)
以上より、与えられたボゴモルニー方程式の解は
\(\begin{equation}\phi\left(x\right)=m\: {\rm tanh}\left(\sqrt{2\lambda m^2}\left(x-\alpha\right)\right)\: \left(\alpha\in{\bf R}\right)\end{equation}\)
記事に戻る: φ^4 kinkをアニールしてみた
プロットしてみ!?
ちなみに\(\alpha=0\)に対してプロットすると、こんな感じ↓
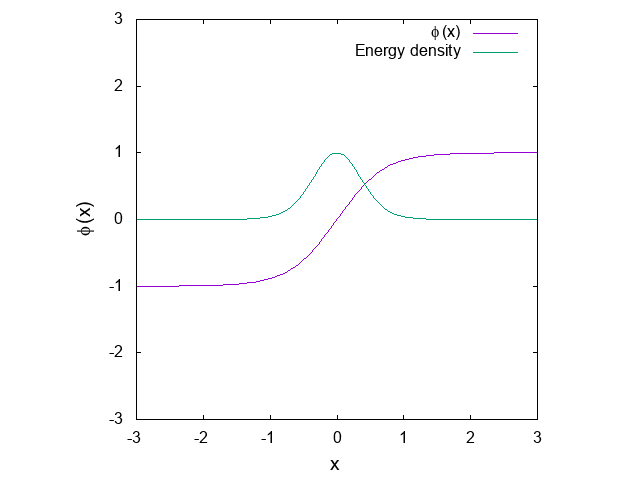
記事に戻る: φ^4 kinkをアニールしてみた
最後に
他にも色々とシミュレーションに関する記事を書いています。ぜひ読んでみて下さい!
→「シミュレーション」一覧
冒頭で使った画像は無料画像提供サイトPixabayさんからダウンロードしました。いつもありがとうございます!(最後のグラフはgnuplotで自分で書いたやつです)
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ下部のコメント欄・上部のお問い合わせフォーム、または下記メールアドレスまでご連絡いただけると大変ありがたいと思います。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。



