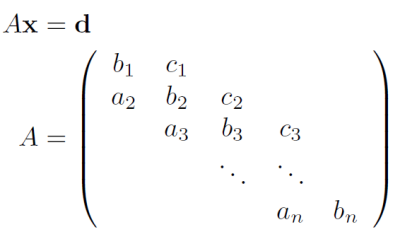実装例付き!3重対角行列を係数行列とする連立一次方程式の解き方

今回は3重対角行列の解き方についてご紹介いたします。

次回の記事で反応拡散方程式についてご紹介する予定なので、その前準備として書きます。

以下のような流れで説明していきます。

3重対角行列
解き方
実装例
例題
まとめ

シミュレーション関連の記事は他にも書いているので、読んでみて下さい。

3重対角行列

3重対角行列とは主対角線とその上下に隣接する対角線にだけ非零の成分を持つ行列のことを言います。(Wikipedia)

\(\begin{eqnarray} A = \left( \begin{array}{ccccc} b_{1} & c_{1} & & & \\ a_{2} & b_{2} & c_{2} & & \\ & a_{3} & b_{3} & c_{3} & \\ & & \ddots & \ddots & \\ & & & a_{n} & b_{n} \\ \end{array} \right) \end{eqnarray}\)

空欄は全て0要素です。
3重対角行列を係数行列とする連立一次方程式は\(O\left(n\right)\)(\(n\)は行列の大きさ)の解法が知られています。ここではそれを紹介します。

解き方

3重対角行列\(A\)を係数行列とする連立一次方程式

\(\begin{eqnarray} A{\bf x} = {\bf d} \end{eqnarray}\)

を解くことを考えます。ここで\({\bf x},\,{\bf d}\)はともに\(n\)次元ベクトルとします。

結論を先に述べますと、

\(\begin{eqnarray} P_{1} &=& -\frac{c_{1}}{a_{1}} \\ Q_{1} &=& \frac{d_{1}}{a_{1}} \\ P_{i} &=& -\frac{c_{i}}{b_{i}+a_{i}P_{i-1}} \\ Q_{i} &=& \frac{d_{i}+a_{i}Q_{i-1}}{b_{i}+a_{i}P_{i-1}} \end{eqnarray}\)

なる\(P_{i},\,Q_{i}\)を用いて

\(\begin{eqnarray} x_{n} &=& Q_{n} \\ x_{i} &=& P_{i}x_{i+1}+Q_{i} \end{eqnarray}\)

と解けます。従って3重対角行列の連立一次方程式は\(O\left(n\right)\)で解けることになります。

まず、一行目に着目します。

\(\begin{eqnarray} b_{1}x_{1}+c_{1}x_{2} = d_{1} \end{eqnarray}\)

より、

\(\begin{eqnarray} x_{1} = -\frac{c_{1}}{b_{1}}x_{2}+\frac{d_{1}}{b_{1}} \end{eqnarray}\)

ここで後々のために\(P_{1} = -c_{1}/b_{1},\,Q_{1} = d_{1}/b_{1}\)とおき、

\(\begin{eqnarray} x_{1} = P_{1}x_{2}+Q_{2} \end{eqnarray}\)

と書いておきます。

次に2行目に着目します。

\(\begin{eqnarray} a_{2}x_{1}+b_{2}x_{2}+c_{2}x_{3} = d_{2} \end{eqnarray}\)

先ほどの\(x_{1}\)の式を代入して整理すると

\(\begin{eqnarray} x_{2} = P_{2}x_{3}+Q_{2} \end{eqnarray}\)

ただし、

\(\begin{eqnarray} P_{2} &=& -\frac{c_{2}}{a_{2}P_{1}+b_{2}} \\ Q_{2} &=& \frac{d_{2}-a_{2}Q_{1}}{a_{2}P_{1}+b_{2}} \end{eqnarray}\)

同じようにすると\(n-1\)行目までは

\(\begin{eqnarray} x_{i} &=& P_{i}x_{i+1}+Q_{i} \\ P_{i} &=& -\frac{c_{i}}{a_{i}P_{i-1}+b_{i}} \\ Q_{i} &=& \frac{d_{i}-a_{i}Q_{i-1}}{a_{i}P_{i-1}+b_{i}} \end{eqnarray}\)

と書けます。\(n\)行目に着目すると

\(\begin{eqnarray} a_{n}x_{n-1}+b_{n}x_{n} = d_{n} \end{eqnarray}\)

ですが、\(n-1\)行目の方程式

\(\begin{eqnarray} x_{n-1} &=& P_{n-1}x_{n}+Q_{n-1} \\ \end{eqnarray}\)

と連立することで

\(\begin{eqnarray} x_{n} = Q_{n} \\ x_{n-1} = P_{n-1}x_{n}+Q_{n-1} \end{eqnarray}\)

を得ます。

以上より、まず\(P_{i},\,Q_{i}\)を前計算で求めておくことで解\(\{x_{i}\}\)が\(O\left(n\right)\)で求まります。

実装例

個人的な実装は以下のような感じです。
もっとこうした方が良いんでねぇかというご指摘はいつでも大歓迎です。よろしくお願いします。

void trimat_sol(double **A,double *a,double *u,int n){
  A[0][1] = -A[0][1];
  for(int i = 1;i<n-1;i++){
    A[i][i-1] = -A[i][i-1];
    A[i][i+1] = -A[i][i+1];
  }
  A[n-1][n-2] = -A[n-1][n-2];

  double *P,*Q;
  if((P = (double *)malloc(sizeof(double)*n))==NULL){
    printf("*** Allocation ERROR P ***\n");
    exit(1);
  }
  if((Q = (double *)malloc(sizeof(double)*n))==NULL){
    printf("*** Allocation ERROR Q ***\n");
    exit(1);
  }
  
  double den;
  double num;
  P[0] = A[0][1]/A[0][0];
  Q[0] = a[0]/A[0][0];
  for(int i = 1;i<n;i++){
    den = A[i][i]-A[i][i-1]*P[i-1];
    P[i] = A[i][i+1]/den;
    num = a[i]+A[i][i-1]*Q[i-1];
    Q[i] = num/den;
  }

  u[n-1] = Q[n-1];
  for(int i = n-2;i>=0;i--){
    u[i] = P[i]*u[i+1]+Q[i];
  }
  free(P);
  free(Q);
}

例題

\(\begin{eqnarray} A &=& \left( \begin{array}{cccc} 2 & 1 & 0 & 0 \\ 1 & 2 & 1 & 0 \\ 0 & 1 & 2 & 1 \\ 0 & 0 & 1 & 2 \\ \end{array} \right) \\ {\bf d} &=& \left( \begin{array}{c} 3 \\ 6 \\ 9 \\ 10 \\ \end{array} \right) \end{eqnarray}\)

答え

\(\begin{eqnarray} {\bf x} = \left( \begin{array}{c} 0.4 \\ 2.2 \\ 1.2 \\ 4.4 \\ \end{array} \right) \end{eqnarray}\)