Warshall-Floyd法 (ワーシャルフロイド法)

今回も競プロネタです。

Warshall-Floyd法はグラフが与えられたときに全頂点ペア間の最小距離を求める方法です。

考え方を理解しておくために記事を書くことにしました。
未来の自分と、このブログにたまたまたどり着いた幸運な(?)読者の方に参考になれば幸いです。

また、競プロ関連の記事は他にも書いています。今後必要なことを拡充していきたいと思いますので参考にしてみて下さい！
→「プログラミングコンテスト」一覧

Warshall-Floyd法とは
実装例
まとめ

Warshall-Floyd法とは

ワーシャル–フロイド法 (英: Warshall–Floyd Algorithm) は、重み付き有向グラフの全ペアの最短経路問題を多項式時間で解くアルゴリズムです。 (Wikipedia)

以下のような4つの頂点からなる最短経路問題を考えます。

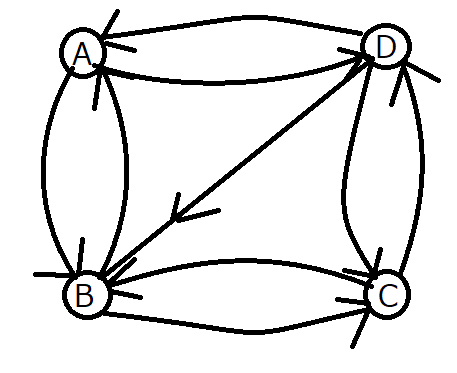
各矢印には移動距離等に相当するコスト \(c_{ij}\) が定義されているものと思って下さい。

Warshall-Floyd 法では始点・終点と中継点を全探索することで各頂点ペア間の最小距離を求めていきます。
例えばAからCまでの最小距離を求めるとき、始点をA、終点をCとして
A -> D -> C
A -> B -> C
A -> D -> B -> C
という3通りが考えられます。

すなわち中継点としてBやDが考えられ、また、Bを中継点として選んだ時、さらにDを経由する方法も考えられます。
ここでBまでの最適な経路が分かったとするとそこからCまでの最適な経路を求めることが出来ます。
従って、AからCまで行きたいとき、全体として最適な経路はその途中も最適になっているという構造が見えます。
いわば動的計画法のように各ペアの最小距離を求めるのがWarshall-Floyd法と言えそうです。
経路を全探索すると\(O\left(2^n\right)\)(\(n\): 経路の数)かかってしまいますが、ワーシャルフロイド法では頂点を全探索することで\(O\left(V^3\right)\)で済みます。

実装例

Warshall-Floyd法の実装は非常にシンプルです。

vector<vector<int>> Warshall_Floyd(int v, vector<vector<int>> graph){
  vector<vector<int>> cost = graph;
  for(int k = 0;k < v;k++){
    for(int i = 0;i < v;i++){
      for(int j = 0;j < v;j++){
          cost[i][j] = min(cost[i][j],cost[i][k]+cost[k][j]);
        }
      }
    }
  }

  return cost;
}

頂点数 \(v\) と重み付き有向グラフ graph を受け取り、各ペア \(i,j\) の最小コスト cost[i][j] を返す関数です。
graph について、張られていない辺のコストは graph[i][p] = \(\infty\) と定義されているものとし、同じ辺同士では graph[i][i] = 0 と定義されているものとしました。
中継点 \(k\) とし、始点・終点 \(i,j\) でループを回し答えを計算します。