今回も競プロネタです。
何かネットワークが与えられたときに、ある頂点から各頂点に行くときの最小コストが気になることがあります。
このような問題を効率的に解くときの手法の一つが幅優先探索です。
幅優先探索(BFS: Breadth First Search)はよく出てくる方法ですが、よく忘れるのと、考え方を理解しておくために記事を書くことにしました。
未来の自分と、このブログにたまたまたどり着いた幸運な(?)読者の方に参考になれば幸いです。
また、競プロ関連の記事は他にも書いています。今後必要なことを拡充していきたいと思いますので参考にしてみて下さい!
→「プログラミングコンテスト」一覧
BFSとは?
幅優先探索(はばゆうせんたんさく、英: breadth first search)はグラフ理論において木構造やグラフの探索に用いられるアルゴリズムです。(Wikipedia)
ネットサーフィンをすることを考えてみましょう。
各サイトは互いにリンクを張ってネットワークを構成しています。
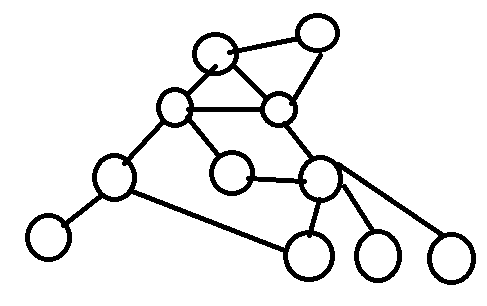
Google先生に何か聞くと検索結果の一覧が表示されますね。
BFSはその検索結果全てを最初に開いて、各サイトを順番に見に行くイメージです。
これに対し深さ優先探索(DFS)という手法もあって、どれか一つのサイトに行って、そのサイトの中のリンクをどんどんたどっていくイメージです。
どちらもサイトのリンクを全てたどるというところは同じですが、
BFSは名前の通り幅広く探索するのに対して、
DFSは貪欲に自分の欲望に任せて一つのサイトのリンクをたどっていくイメージです。

1番のサイト(例えば検索結果一覧)から赤い矢印で行けるサイトを全て訪問して、その後にその中のどれかから行けるサイトを青い矢印のようにすべて訪問して・・・ということを繰り返します。
各サイトを訪問したかどうかを検査しながら探索していくことで、各サイトを高々1回しか訪問しないため、全てのサイトを\(O\left(N+M\right)\)(\(N\): サイト数、\(M\): リンク数)で全てのサイトを訪問することが出来ます。
相性の良いデータ構造と遷移の様子
BFSはC++のQueueというデータ構造と相性が非常に良いです。
Queueというのはデータを入れる方向と出す方向が一方通行になっているデータ構造です。
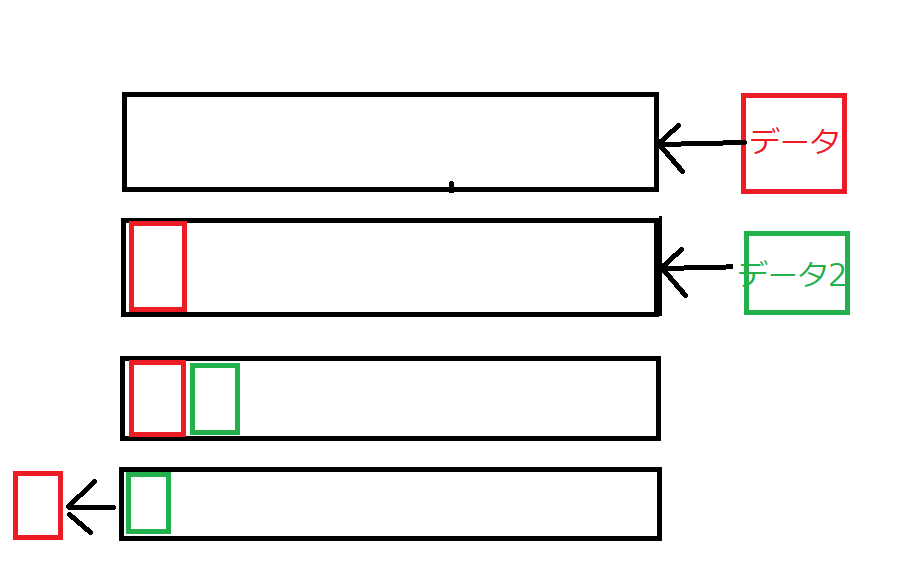
上記で言うと「データ2」を「データ」より先に取り出すことはできません。
この構造がBFSと非常にマッチします。
Queueに訪問したサイトがつながっているサイトの番号を突っ込んでいき、次に訪問するサイトを決めるときにQueueの先頭の番号を取り出せば順次枝葉を探索していくことができます。
先ほどの例で言えば、[]でQueueのデータ構造を表したとき、以下のように遷移していくことになります。
[1] -> [] -> [3,4,2] -> [4,2] -> [4,2,5,6] -> [2,5,6] -> [2,5,6,7] -> [5,6,7] -> [6,7] -> [6,7,8,9] -> [7,8,9] -> [8,9] -> [8,9,10,11] -> [9,10,11] -> [10,11] -> [11] -> []
実装例
void bfs(vector<vector<int>> &Graph, vector<int> &dist){
for(int i = 0;i<n;i++) dist[i] = -1;
queue<int> q;
dist[0]=0;
q.push(0);
while(!q.empty()){
int v = q.front();q.pop();
//if(dist[v]!=-1) continue;
for(auto nv : Graph[v]){
if(dist[nv]!=-1) continue;
dist[nv]=dist[v]+1;
q.push(nv);
}
}
}ネットワークを表すGraphという配列とある頂点から見た距離を表すdistという配列を渡します。distを-1で初期化しておくことで訪問済かどうかの判定に使います。
今回は頂点0から探索を始めることにしてdist[0]を距離0とし、queueに頂点0を追加します。
あとはqueueが空になるまで探索を繰り返し、各頂点の距離を保存しておきます。
これにより頂点0から各頂点への最小距離が分かります。
まとめ
いかがだったでしょうか。
今回は今後の自分のためと、同じような悩みを抱えている方向けにBFSのやり方・考え方を書いてみました!
誰かのお役に立てれば幸いです。
また、DFSで閉路検知に挑戦した記事もありますので良かったら読んでみて下さい!
→DFS (Depth First Search)で閉路検出。実装例付き!
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。
サムネイル画像はpixabayさんからダウンロードさせていただきました!
ありがとうございます!



