DFS (Depth-First Search)で閉路検出。実装例付き！

今回は閉路検出をDFSで実装してみましょうという企画です！
個人的に再帰に苦手意識があり、
また同じようなこと(閉路検出に限らず)はBFSでもできるので今まで避けてきましたが、
BFSよりDFSの方が実装しやすいなーと思うことが出てきたのでこれを機にお勉強しようと思った次第です。

以下のような流れで説明していきますので参考にしてください！

DFSとは？
閉路検出の考え方
実装例
まとめ

DFSとは？

DFSはグラフを探索するアルゴリズムです。
グラフとは点と棒がつながった以下のようなものです。

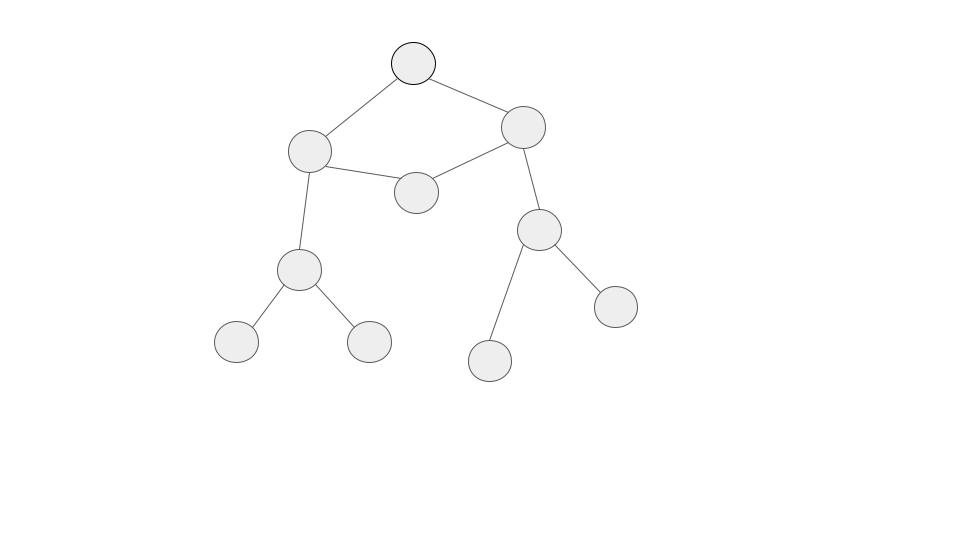
例えばネットサーフィンをすることを考えてみましょう。
各サイトは互いにリンクを張ってネットワークを構成しています。

Google先生に何か聞くと検索結果の一覧が表示されますね。
DFSはどれか一つのサイトに行って、そのサイトの中のリンクをどんどんたどっていくイメージです。

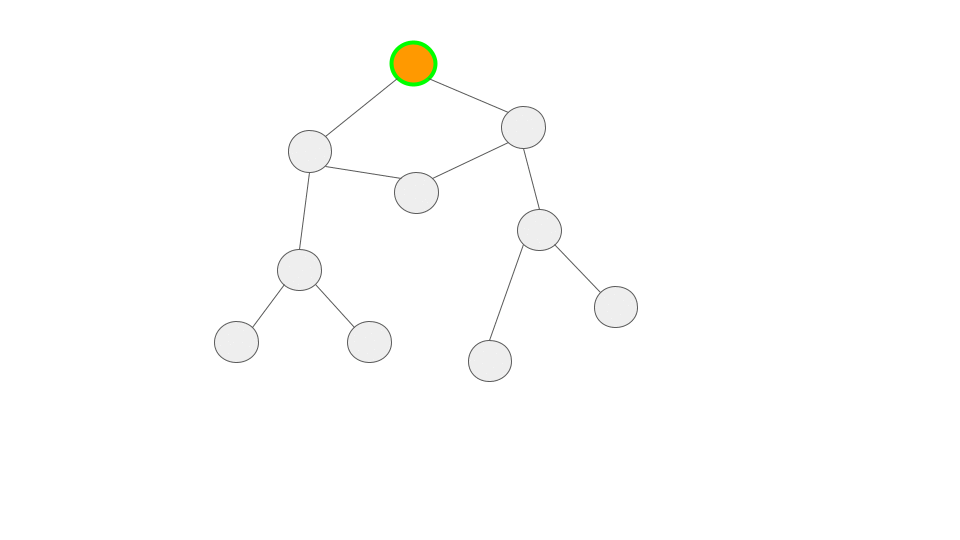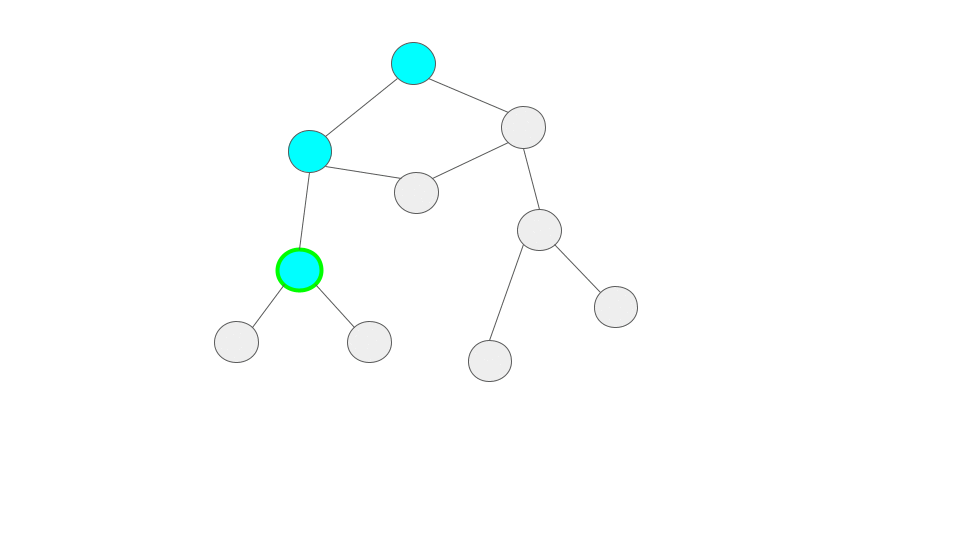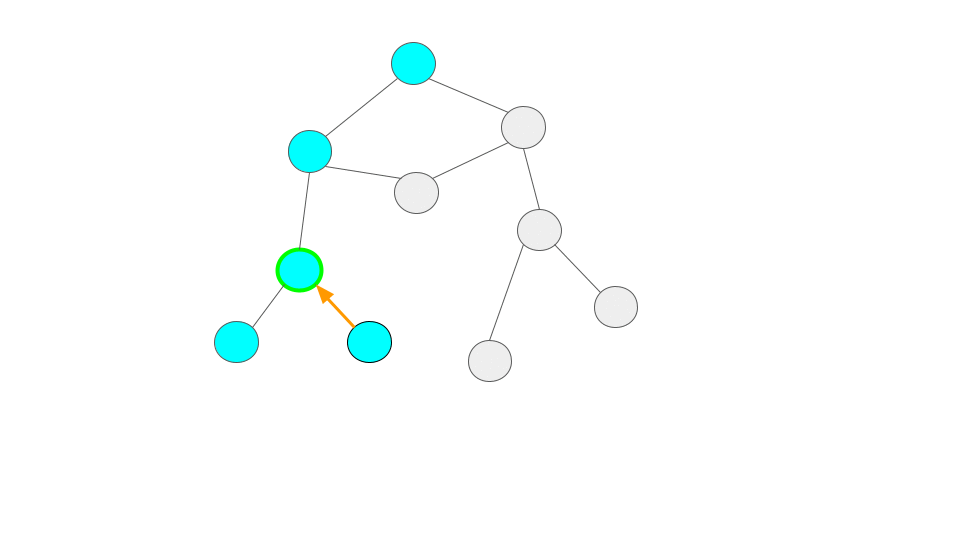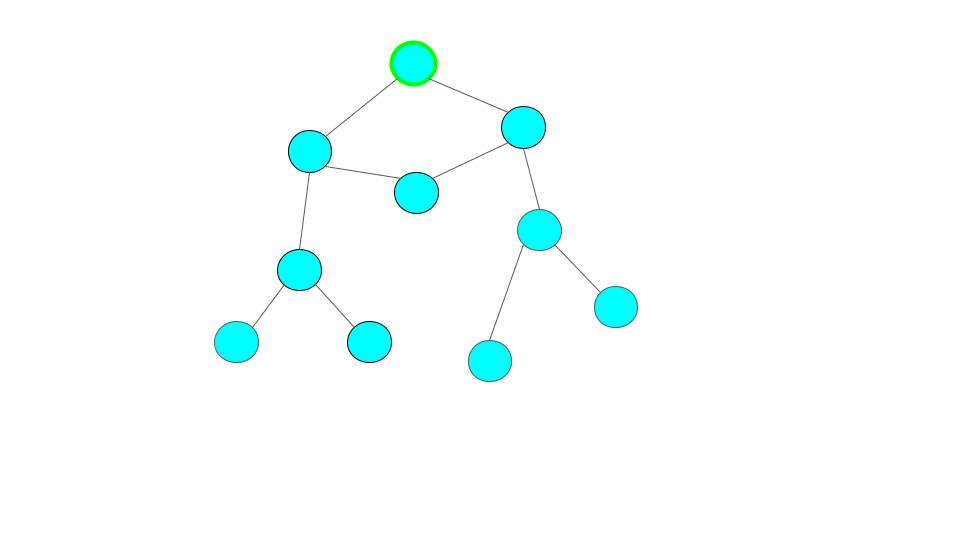
緑の縁でユーザが今いるサイトを表しています。
また、訪問済のサイトを水色、訪問先のサイトをオレンジで表現しています。
サイトのリンクをたどっていってリンク先がなくなったら一つ戻って別のリンクに行きます。
この動画のように、猪突猛進でリンクを辿りながら全てのサイトを訪問する方法がDFSです。

各サイトを訪問したかどうかを検査しながら探索していくことで、各サイトを高々1回しか訪問しないため、全てのサイトを\(O\left(N+M\right)\)(\(N\): サイト数、\(M\): リンク数)で全てのサイトを訪問することが出来ます。

閉路検出の考え方

まず閉路とは、始点と終点が同じ道のこと。すなわち、出発点に戻るような辿り方であって頂点の重複がないグラフのことです。(Wikipedia)
先ほどの例で言えば、以下の赤い線でつながった道が閉路です。

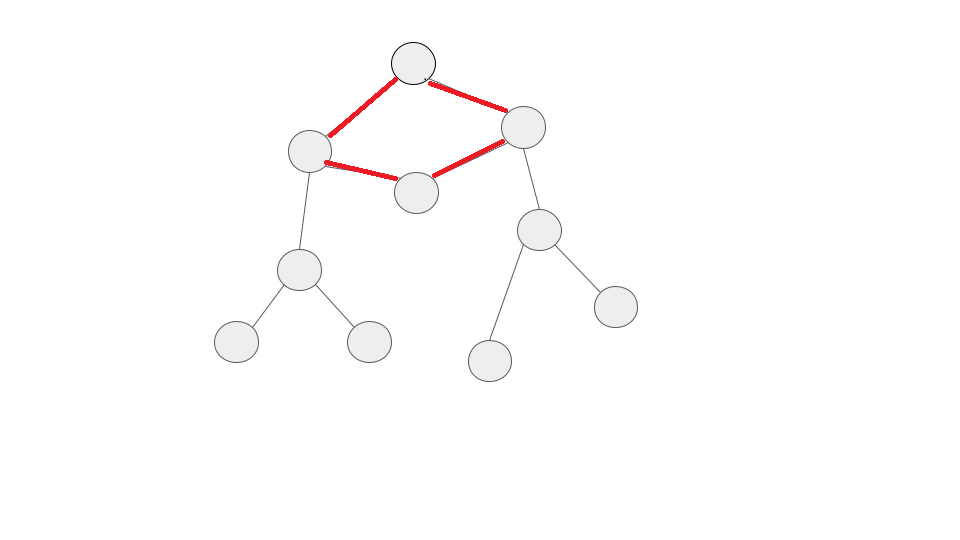
グラフに閉路があるとき、ある頂点から探索していくと必ずすでに訪れた頂点を通ることになります。

なのでDFSによる閉路検出では、ある頂点を探索したかどうかという情報を持ちながら探索し、一度訪れた頂点を発見した時点で閉路ありと判定します。

実装例

bool Cyclic_DFS(const vector<vector<int>> &G, int v, vector<int> seen){
  seen[v] = 0;

  for(auto next_v : G[v]){
    if(seen[next_v] == 0) return false;
    else if(seen[next_v] == -1){
      if(!CyclicDFS(G,next_v,seen)) return false;
    }
  }
  seen[v] = 1;
  return true;
}

まず、頂点の状態を3状態で管理します。

-1: 未訪問
0: 訪問済かつスタックに積まれている
1: 訪問済かつスタックから除かれている

一つ注意しなければならない点は訪問済の頂点について、今回っている経路上にあるかどうかを判定するためさらに2状態に分けなければならない点です。
これは以下のグラフを見るとよく分かります。

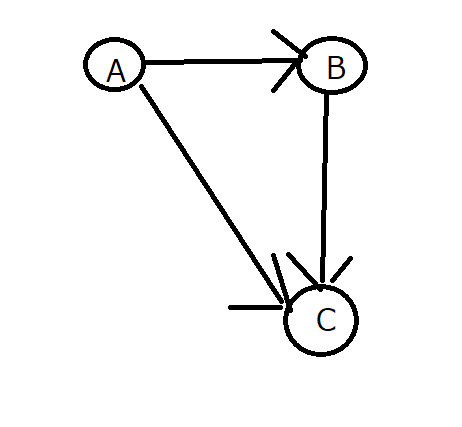
上記のような有向グラフの場合、閉路はありませんが全ての頂点を訪問済にすることはできてしまいます。
訪問済という情報のみを管理しているとこのようなグラフも閉路と判定されてしまうのです。
閉路検出をするためには訪問済の頂点が今通っている道の途中にあるのか否かという情報 (つまり訪問済の頂点がまだスタックにあるか否か)も保持しておく必要があります。
これが上記実装における数値0と数値1の違いです。