3次元球の体積を求める

今回は\(n\)次元球の体積に向けて
3次元球の体積をなるべくわかりやすく求めてみようという企画です。
関連記事: 考え方を徹底解説!n次元球の体積を求めよう!

少々酔っぱらいながら書いているので、若干間違っていることもあるかもしれません。
今日の忘年会は楽しかった！！

以下のような流れで書いていきます。

3次元球の体積を求めてみる
高校時代の自分の話~積分は面積を出すもんだと思ってた~
まとめ

3次元球の体積を求めてみる

高校くらいで習うように、3次元球の体積は

\(\begin{eqnarray}V_{3}=\frac{4}{3}\pi r^{3}\end{eqnarray}\)

です。\(V_{3}\)と書いたのは3次元の球の体積ですよ、ということを明示するためです。

この公式は一体どこから来たのでしょう。

いきなり球の体積は無理なのでまずは2次元で考えましょう。

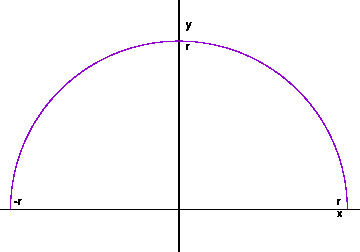
この半円を\(x\)軸で回転させてできる立体は球です。

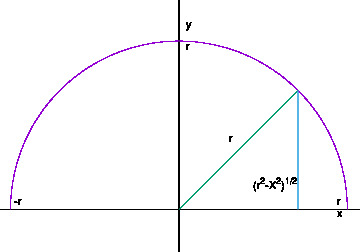
青い線を一回転させると半径\(\xi = \sqrt{r^2-X^2}\)の円ができます。

位置\(X\)にある、青い線を\(x\)軸周りで回してできる円の面積は\(\xi = \sqrt{r^2-X^2}\)として\(\pi \xi^2\)と書けます。\(x\)軸方向に厚さ\({\rm d}X\)を持つ円盤を考えると、その体積は\(\pi \xi^2{\rm d}X\)です。従ってできる球の体積は、この円盤の体積を\(X\in\left[-r,r\right]\)で足していけば良いので

\(\begin{eqnarray} V_{3} &=& \int_{-r}^{r}\pi\xi^2 {\rm d}X \\ &=& \pi\int_{-r}^{r}\left(r^2-X^2\right){\rm d}X \\ &=& \pi \, 2\int_{0}^{r}\left(r^2-X^2\right){\rm d}X \\ &=& 2\pi\left[r^2X-\frac{1}{3}X^3\right]^{r}_{0} \\ &=& 2\pi\left(r^3-\frac{1}{3}r^3\right) \\ &=& 2\pi\frac{2}{3}r^3 \\ &=& \frac{4}{3}\pi r^3 \end{eqnarray}\)

いわゆるバームクーヘン積分みたいなものですね。

高校時代の自分の話~積分は面積を出すもんだと思ってた~

なんかものすごく簡素な感じになってしまったので
私の高校時代のお勉強の話をしてみようと思います。

私自身は高校時代、そんなにお勉強ができる方ではありませんでした。
模試は大体校内7位とかそんくらいが最高でした。

そんな私の最大の勘違いの一つが積分に関するものでした。

当時の私は積分といえば面積を出すもの、と思っていました。
学校の課題でも、積分で求めるのはあるグラフと\(x\)軸とで囲まれる領域の面積ばっかり。
そんなこんなで演習を重ねていくうちに、いつしか積分は面積を求めるもんなんだと勝手に思い込んでしまっていたんですね。
まぁ、そんな勉強でも覚えてしまえば大学には受かってしまうんですね。
(保証はしません。ラッキーを狙わずにきちんと数式の意味とかを考えて勉強してくださいね)

この考えが間違っていたことに気づくのは大学に入ってからです。
教授の書いた以下の数式の意味が全く分からなかったのです。

\(\begin{eqnarray} M &=& \int{\rm d}m \\ &=& \int\rho{\rm d}V \end{eqnarray}\)

\(M\)はある物の質量です。
まぁ、そりゃ積分が面積を出すもんだと思っている輩には分かるわけがありません。

今考えれば笑ってしまうような話なのですが、当時の私は真面目な顔して先生に聞きに行きました。
マジか、みたいな顔をされましたが、やさしく丁寧に教えていただいたのはいい思い出です。

まとめ

いかがだったでしょうか。

今回は次回の\(n\)次元球の求積に向けてのウォーミングアップでした。
(関連記事: 考え方を徹底解説!n次元球の体積を求めよう! )
大学入試等ではここまで基本的な問題は逆に出ないかもしれませんが(3次元の話)、求積や基本的な問題では微小区間に分けてから後で足すというのは常套手段なので覚えておいて損はないと思います。

他にも色々とお役立ち情報を書いています。参考にしてみて下さい！
→「数学」一覧

最後まで読んでいただきありがとうございました！！

もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。

tsunetthi(at)gmail.com

(at)の部分を@に変えてメールをお送りください。

または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。