毛細管現象とそれを利用した自動水やり機について

今日からバジルを育てていくことにしました！
去年は失敗してしまったので、今年こそはおいしいバジルを収穫してガパオライスに添えたいと思います！

ここでは、
・長期間家を空けるときに重宝する¹水やりを自動化してくれる装置の紹介
・その原理の一つとして毛細管現象について紹介します。

以下のような流れで説明していきます。

バジル育成1日目！
ところで長期間家を空けるときどうしようか
毛細管現象
毛細管現象で吸い上げられる流体(水)の高さの限界
まとめ

バジル育成1日目！

近くの園芸ショップに行ってバジルの苗を買ってきました！
今日は風が強かったので、
帰りの道すがらせっかく買った苗が飛ばされないか心配でしたが、
なんとか家まで持ち帰ってくることができました。

帰るや否やさっそくプランターの土を入れ替え、鉢底石とハーブ用の土を投入。
やさしくバジルの苗を植え、水をあげつつおいしくなる呪文を唱えました。

今後の生長に期待しつつ、去年と同じ失敗だけはしないように育てていきたいと思います。

ところで長期間家を空けるときどうしようか

バジルを育てるのはいいんですが、
旅行や帰省などで長期間家を空けなければならないとき、水やりはどうすればよいでしょうか。
もちろん、今は時期が時期ですのでそんな心配はかえって無用なのですが
いつかは収束(and 終息)しますから、そのときのために対策を考えておこうと思うわけであります。

世の中にはそんなときのために、自動で植物に水をあげる装置が非常にたくさんあります。
電気を利用してなんか自動でやってくれたり

セフティー3 自動水やり器電池式タイマースタンド付 1日4回まで対応芝生・鉢植え・畑用 SAW-2 & セフティ3 ホース分岐コネクタ SSK-6【セット買い】

毛細管現象という自然現象を利用したクリーンなものがあったり

水やり当番自動水やり器給水ツール園芸用品留守中盆栽鉢植え繰り返し使用自動給水装置水遣り機自動散水システム (M（5個セット）)

他にもなんか似たようなのがたくさんあります。

値段も安いしとっつきやすそうなので
今回は毛細管現象を利用した方法で対策を考えていきたいと思います！

毛細管現象

みなさん、毛細管現象という言葉は聞いたことがありますか？
植物が体内の水を隅々まで運ぶのにこの現象を利用しているということは、確か理科で習いますね。

これは非常に細い管の中を水などが登っていく現象です。
例えば、コップに水を入れてひっくり返すと水は床にぶちまけられるわけでありますが
そこへ非常に細いストローなどを入れておくと水が勝手に上へ上へと上がっていく、とても面白いことが観察できるわけですね²。

さて、この毛細管現象を利用すれば、長期間家を空けた時の水やり対策ができます。
具体的には、バケツに水を張っておいて非常に細い管を入れて置き、
その出口をプランターの土に差しておけばいいわけです。
しかしながら、ここで色々と考えなければならないことがあります。

一つはどのくらいの量の水を張っておけば良いかです。
もちろん、家を空ける期間が長ければ長いほど用意しておかなければならない水の量は増えるでしょう。
また、実は毛細管現象で水を吸い上げられる高さには限界があります。
つまり、何も考えずに適当に装置を組んでしまうと
水を吸い上げる高さが足らずに、バジルが枯れてしまう可能性があるんですね。

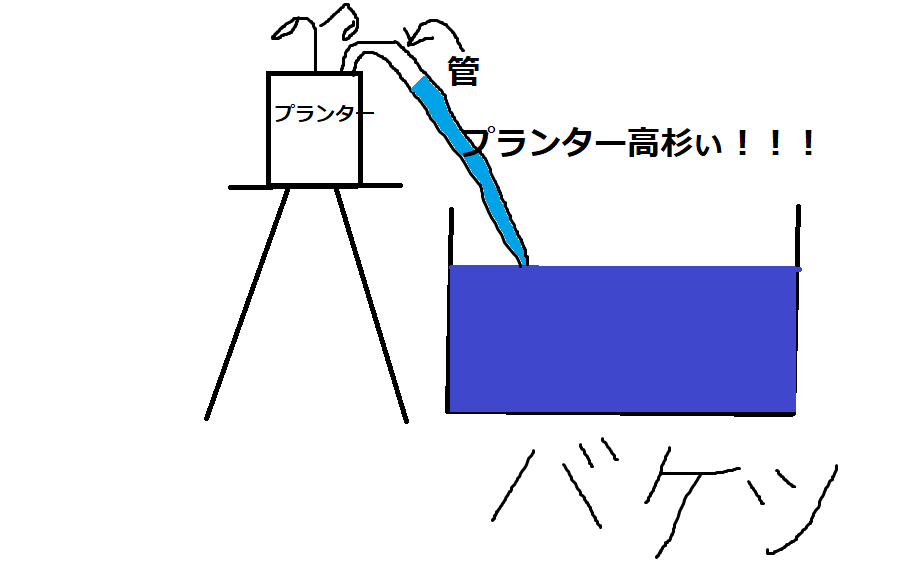
プランターが高すぎると水が届かない — プランターが高すぎて水が届かんのじゃぁ！

今回は特に水を吸い上げる高さの限界に注目して、色々と考えていこうと思うわけであります。

毛細管現象で吸い上げられる流体(水)の高さの限界

バケツにためた水を高さ\(h\)まで毛細管現象によって吸い上げることを考えます。管の直径を\(2r\)と書きます。

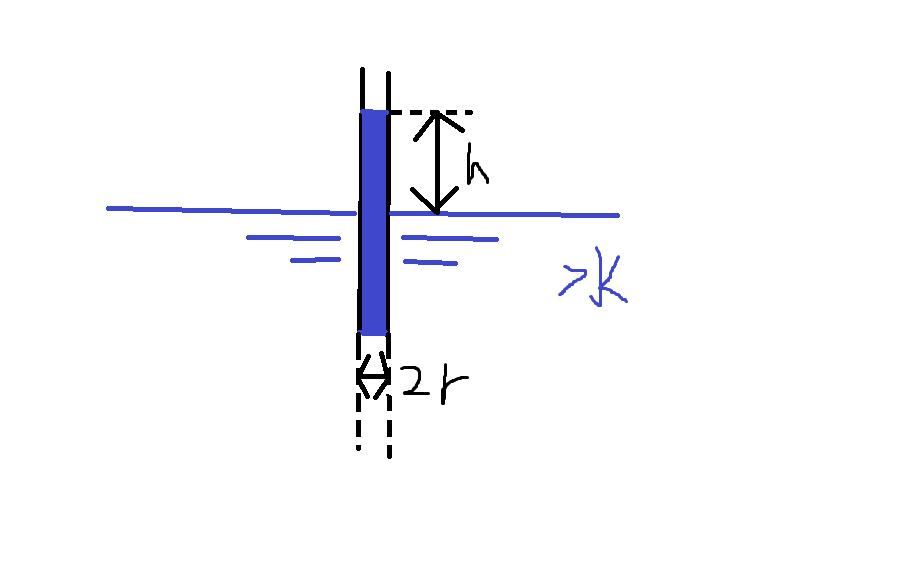
半径rの円柱の中、水面から高さhに水が上がる — 直径\(2r\)の細い管を使って高さ\(h\)まで水を吸い上げます

さて、水には表面張力というものがあります。
水の表面積をできるだけ小さくするような働きをするものです。
そして体積一定のもとで表面積が最小になる形というのは球であります
[enf_note]この辺を納得していただくための記事を書いています。少々お待ちください。とにかくここでは表面積最小の形は球ということにして先に進みます。[/efn_note] 。

みなさん、コップに水を注いでみると水の表面が平坦ではなくコップ側面では盛り上がっていることに気づくと思います。

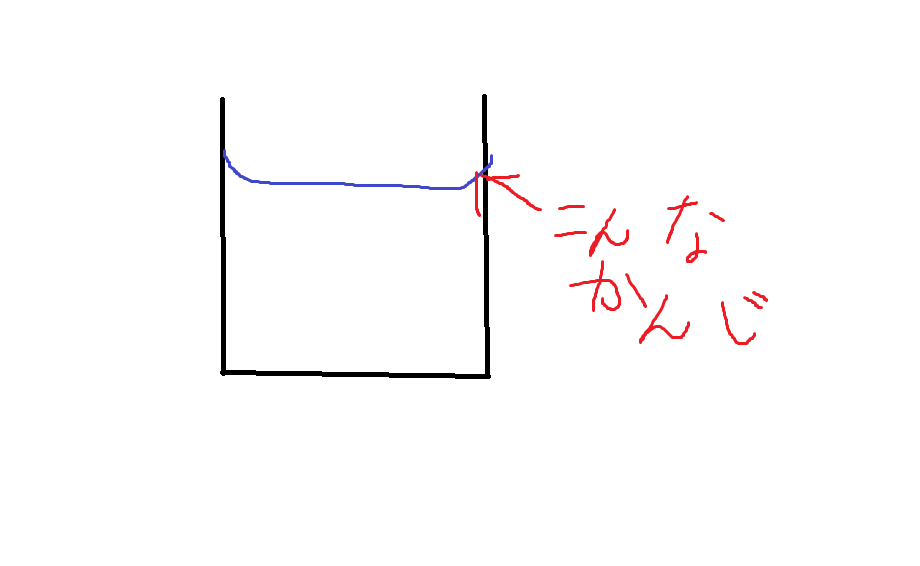
これは表面張力によって水の表面が球になろうとしていることの表れなんですね。

さて、細管が水を吸い上げる高さの限界を考えていきましょう。
管の水面には表面張力と重力(とそれから大気圧)がかかっています。

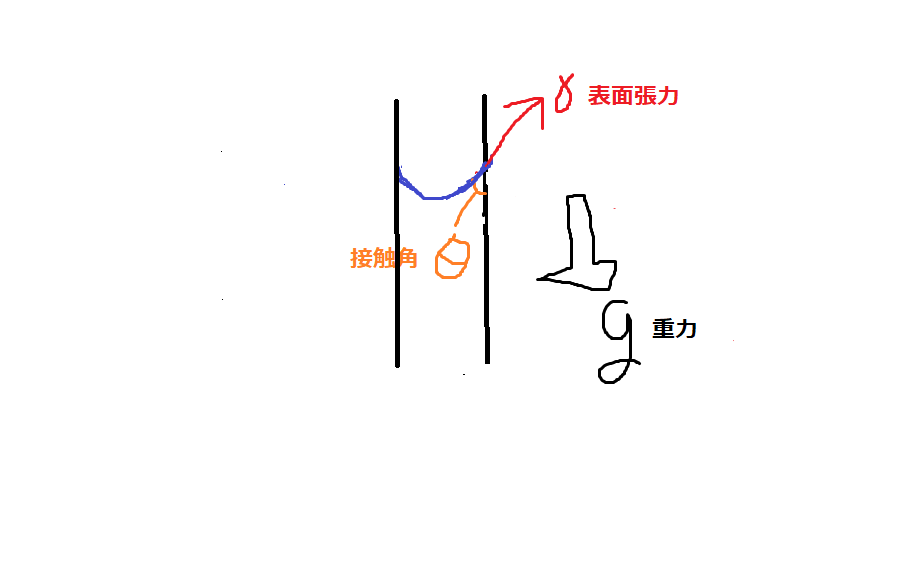
水面が上昇していくと、段々と水の量が増えてきますので
表面張力の上向き成分の大きさと重力が釣り合ったところで
水面の上昇が止まると考えられます。

重力の方は水の密度を\(\rho\)とすると

\(\begin{eqnarray} W = \rho g h\pi r^{2} \end{eqnarray}\)

これに対して表面張力の鉛直成分の方は
管の円周に沿って単位長さ当たり\(\gamma\)の力がかかっているので

\(\begin{eqnarray} F = 2\pi r\gamma\cos\theta \end{eqnarray}\)

この二つが釣り合うので

\(\begin{eqnarray} 2\pi r\gamma\cos\theta &=& g\rho\pi r^{2} h \\ h &=& \frac{2\gamma}{\rho g r}\cos\theta \end{eqnarray}\)

この式によると管の半径が小さいほど高く水が吸い上げられるということがいえます。
試しに1cm の高さに水を上げるのに必要な管の細さを求めてみましょう。
常温の水の表面張力は\(\gamma = 72.75\times \,10^{-3}\,{\rm N/m}\)³、密度は\(\rho \simeq 1\,{\rm g}/{\rm cm}^3 = 1000\,
{\rm kg}/{\rm m}^3\)重力加速度が\(g\simeq 9.8\,{\rm m}/{\rm s}^2\)、接触角が一番難しいですが体感的に\(\theta\simeq\)30°くらいにしておきましょう。

\(\begin{eqnarray} h &=& \frac{2\gamma}{\rho g r}\cos\theta \\ r &=& \frac{2\gamma}{\rho gh}\cos\theta \\ &\simeq& \frac{2\times 72.75\times 10^{-3}}{1000\times 9.8\times 0.01}\cos\left(30^{\circ}\right) \\ &\simeq& 1\,{\rm mm} \end{eqnarray}\)

ちょっとこれは要実験な気がしますね。
今回の記事はここで終わりますが、実際に市販の毛細管現象を利用した水やり機を買ってきて、どのくらいの高さまで水を吸い上げることが出来るのか検証してみようと思います。
市販のものは何か工夫があるのかもしれません。

まとめ

いかがだったでしょうか。

今回はバジルを育て始めたよというお話と
自動水やり機の原理の一つである、毛細管現象について紹介しました。

他にもお役立ち情報は色々と書いているので、気になる記事を読んでください！

もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。

tsunetthi(at)gmail.com

(at)の部分を@に変えてメールをお送りください。

または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。

今は時期が時期ですのでそんな心配は無用なのですが、今後必要になるものですので今のうちに知っておこうということです。
上に上がっていかない場合はストローの細さが足りない可能性が高いです
参考URL:
https://japanknowledge.com/contents/nipponica/sample_koumoku.html?entryid=623