Floyd-Warshall algorithm

Hello, guys! It’s me! Warotan!
So…Who are you?→ABOUT ME

Japanese version.

The Floyd-Warshall algorithm is a way to find the minimum distance between all vertex pairs in a given graph.

I decided to write this article to help you understand the concept.
I hope it will be helpful to my future self and to the lucky (?) readers who happened to come across this blog.

Also, I wrote other articles related to competitive programming.
The English version is coming soon. Please wait for it !!

Floyd-Warshall algorithm

The Floyd-Warshall algorithm is a way to find the minimum distance between all vertex pairs in a given graph.

We consider a shortest path problem here.

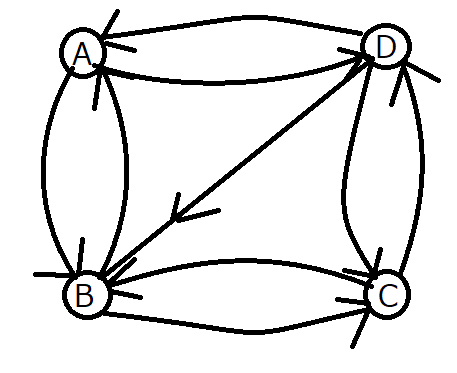
Costs \(c_{ij}\) are defined on each arrow.

In Floyd-Warshall algorithm, we can obtain the minimum distance between each vertex pair by searching all the starting, relay, and ending points.
For example, to find the minimum distance from A to C, letting the starting point be A and the ending point be C, there are 3 ways to reach C,
A -> D -> C
A -> B -> C
A -> D -> B -> C

We can take B or D as a relay point, and if B is taken, there is also a way to relay D.
If we know the best way from A to B, we can find the best way to C from B.
Therefore, when we would like to go from A to C, you can see the structure that if the whole path is optimal, then the middle part of it is also optimal.
As we say, Floyd-Warshall algorithm is a way to find the minimum distance between all pairs like Dynamic Programming.

Implementation example

Floyd-Warshall algorithm is very simple to implement.
The computational complexity is \(O\left(\left| V\right|^3\right)\) as we search all starting, relay, and ending points, \(\left| V\right|\) is the number of vertices.

vector<vector<int>> Warshall_Floyd(int v, vector<vector<int>> graph){
  vector<vector<int>> cost = graph;
  for(int k = 0;k < v;k++){
    for(int i = 0;i < v;i++){
      for(int j = 0;j < v;j++){
          cost[i][j] = min(cost[i][j],cost[i][k]+cost[k][j]);
        }
      }
    }
  }

  return cost;
}

This function returns the minimum cost cost[i][j] for each pair \(\left(i,j\right)\) by taking the number of vertices \(v\) and a weighted directed graph graph.
Here, we consider the cost of unconnected sides is defined as \(\infty\) and graph[i][i] = 0.
The index k represents the relay point and i,j the starting and ending point.

Summary

Now, that’s all what I wanted to write.

This time, I introduced Floyd-Warshall algorithm that finds the minimum distance between all verticex pairs with \(O\left(\left| V\right|^3\right)\).

Thank you for reading and please spread this blog if you like.

If you have any comment, please let me know from the e-mail address below or the CONTACT on the menu bar.
tsunetthi(at)gmail.com
Please change (at) to @.

Or you can also contact me via twitter (@warotan3)