こんにちは!わろたんです!
今回は私がやっていた院試勉強法と、院試時代に使っていた問題集・参考書等を一気に紹介していこうと思います!
気になったものはぜひ使ってみて下さい。
今回の記事の構成は以下のようになっています。
ご自分の興味にあわせて読んでください。
院試受験のときの受験勉強って何してたの?
今回は参考書の特集ですが、その前に受験生の方は興味があるであろう、院試の受験勉強をどうしていたかについてお話します。
どの科目にどの程度時間を割いていたかを時期に応じて説明していきますので、よかったら参考にしてください!!
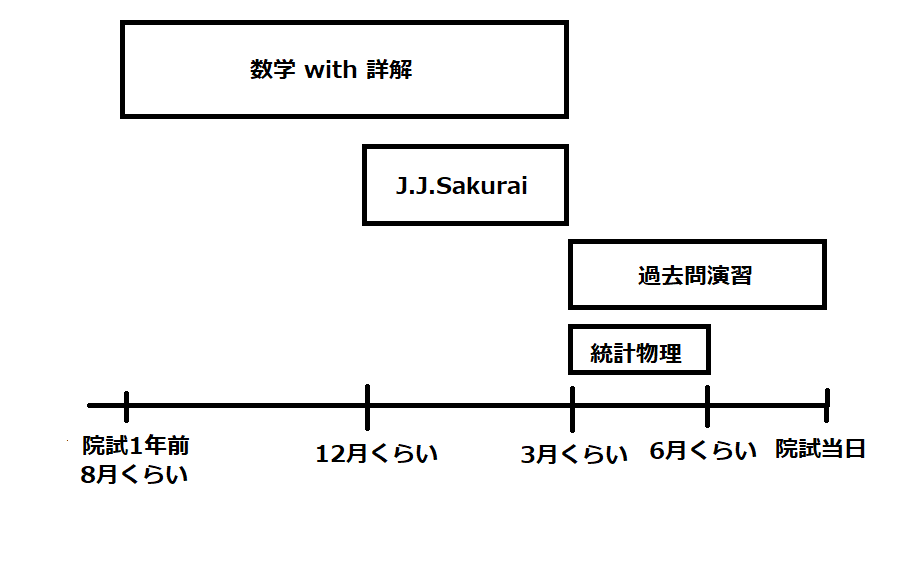
私が院試の勉強をスタートさせたのは、受験の1年前くらいからです。
このくらいの時期になると、周りの友達も院試を意識し始めます。
ある日
週一で院試の勉強会やるけど一緒にどう?
と勉強会に誘われたのが一番最初でした。
このときの友達には感謝しています。
私一人では、多分続かなかったと思うので。
最初は大学の講義室などをこっそり使っていました。
その後、理由は忘れましたが(講義室は勝手に使ってはいけなかったような気がします)何回目からか友達の家に集まって勉強会をすることになりました。
友達の家にはホワイトボードがあって、それに影響されて私も自前のブラックボードを作りました。
最初は数学から始めました。
その時につかっていた参考書は『詳解と演習 大学院入信問題 数学 大学数学の理解を深めよう』(海老原円 著)です。
詳解と演習大学院入試問題〈数学〉: 大学数学の理解を深めよう
これは過去の大学院入試の数学の問題をかき集めて収録した感じになっています。
特徴としては、色々な専攻の過去問が載っているところですかね。
私は物理学専攻を受験しましたが、この本にはそれこそ数学専攻の問題だったり、土木専攻だったり、まぁ色々載っていました。
あみだくじを作って、次の週に誰がどの問題を解説するかを決めてやっていました。
例題からA問題B問題まで全て残さず解きました。あ、最後の確率の問題は解いてません。
中には全然知らない単語ばかりで、なじゃこりゃ?という問題もありますが、そういうのもみんなで戦ってみたりしました。
色々自分たちで考えてみたり、インターネットで調べてみたりして、とても楽しかったのを覚えています。
そんなこんなで、4か月くらいですかね。
年の瀬も近づいてきて、そろそろ物理方面の自主ゼミもしようということでJ.J.Sakuraiの量子力学上下を読み始めました。

現代の量子力学(上)第3版 (物理学叢書112)




第3版 現代の量子力学(下)(物理学叢書, 113)
ここから、週2で自主ゼミが始まりました。
1週間に4節とかいうキチガイなスピードで読もうということになって、3月の中頃にはすでに終わった気がします。
各自1週間後までに、みんなで決めた場所までは読んできて、分からなかったり議論の余地があると思うところをピックアップして議論する。
演習問題もいくつかピックアップして、くじで誰が解説するかを決めて次の週にホワイトボードで解説する。
そんなような感じで進めていました。
一度解説した問題だけは自力で何も見ずに回答の流れを書けるようになることを目標にしていました。
ただ、勉強科目の順番としては間違っていなかったように思います。
先ほどの数学のゼミで線形代数はしっかり身についていたので、あまり抵抗なく読めたと思います。




統計物理学 (現代物理学基礎シリーズ)
こちらは、巨視的現象の確率解釈などの統計力学の非常に基礎的な内容からEinstein凝縮などの応用まで一冊にまとめられた良い本だと思います。
院試受験だけ考えれば統計力学はこの一冊で十分だと思います。
過去問は東大などがホームページで公開しているので是非ダウンロードして使いましょう。
見ていただければわかりますが
統計力学
電磁気 or 力学
実験など
という構成になっています。
実は量子力学が一番点数が取りやすかったりします。
大体出る問題は決まっているので、基本さえしっかり押さえておけばまず落とすことはありません。
統計力学はあまり勉強していなかったので、かなり苦労しました。
それで川勝さんの本を読み始めたわけですが。
あとは、友達にも色々教えてもらいました。
実験は当たって砕けろです。
私の場合は大学の講義でやった内容がそのまま出て、ラッキーでした。
院試直前期はダウンロードした過去問が全部解き終わってしまったので、別の大学院の過去問も少しやっていました。
参考書・教科書って何使ったの?
ここまでであらかた参考書の紹介は終わりなのですが、上で出てきてない参考書もあるので改めてここで紹介します。
- 海老原円:詳解演習大学院入試問題(数学)
- 村上正康: 教養の線形代数5訂版
- ジョージ・アルフケン、ハンス・ウェーバー著/権平健一郎、神原武志、小山直人訳: 基礎物理数学 Vol.3
- 原岡喜重: 数学の風景 超幾何関数
- J.J.Sakurai: 現代の量子力学 上下 物理学叢書
- 川勝年洋: 統計物理学




詳解と演習大学院入試問題〈数学〉: 大学数学の理解を深めよう
色々な専攻の数学の過去問が載っています。
数学はこれ一冊を解ければ、院試は突破できると思います。



教養の線形代数
線形代数はめちゃめちゃ大事です。
院試に限れば、これがあれば良いんじゃないでしょうか。
量子力学でも重要な固有値方程式や、固有ベクトルの直行性などの証明も簡潔にまとめられています。



基礎物理数学第4版Vol.3 特殊関数 (KS理工学専門書)
完全に趣味の範囲ですが、私が最初に特殊関数の勉強をしたのはこの本でした。
上の数学の演習書でも微分方程式を扱う問題はありましたが、この本のおかげでそこは無双でした。
微分方程式を弄ったり、積分区間をゴニョゴニョしたりするのが好きな人はやってみて下さい。
演習問題もたくさんありますので、良い暇つぶしになります。



超幾何関数 (すうがくの風景)
せっかくですので特殊関数関連でもう一つ。
こちらは私が最近まで読み進めていた本です。
微分方程式と対話しながら勉強したい人はおススメです。
敢えて級数解から微分方程式を導くことで、その関数の性質を浮き彫りにするという面白い手法をとっています。
私は3章くらいまでやって、長いこと休憩中ですが、また気が向いたら読み進めたいと思います。




現代の量子力学(上)第3版 (物理学叢書112)




第3版 現代の量子力学(下)(物理学叢書, 113)
Stern Gerlach実験を使って、量子力学の持つ奇妙な性質を説明しています。
これを読めば、確かに直観を放棄せざるを得ないと納得すると思います。
また、ブラケット記法についてもわかりやすく書いてあるので、そこら辺があいまいな人は読んでみると良いのではないでしょうか。




統計物理学 (現代物理学基礎シリーズ)
院試の統計物理はこれ一冊やっとけば良いと思います。
復習が全然できていない人にはおススメです。
分配関数ってなんだっけ?
ボルツマン因子?なんか不味そう
っていうレベルの人でも全然ついていけます。
まとめ
いかがだったでしょうか。
今回は今までとは趣向を変えて、若干真面目な話もしました。
大学受験に比べれば自分の好きなものをやればよいので、気持ちの入り様が全然違いますでしょう。
国語も歴史もいりません。
なんて良いものなんだ!!
最後に、みなさん願書はちゃんと出しましたか?
きちんと期限を意識して早めの行動を心がけましょう。
最後まで読んでいただき、ありがとうございます。
他にも色々と院試関連の記事を書いています。以下リンク先にあるので参考にしてみて下さい!
→「院試」一覧
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。



