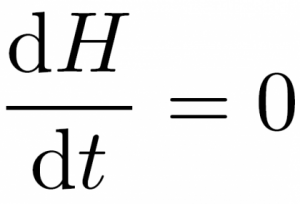今回はロトカ・ヴォルテラ方程式を解くの続編です。
ロトカ・ヴォルテラ方程式系の満たす保存量について書いていきます。
保存量がきちんと保存しているか確認することは、数値計算がちゃんと間違いなく進んでいるか確認するのに役立ちます。(偉そうに言ってますが、前回記事執筆時点では実は保存してませんでした。4次のルンゲクッタ法で解いたのですが、\(k_{i}\)の係数1/2をかけ忘れてて保存量が保存してませんでした。すいません!)
[cmtoc_table_of_contents]
ロトカ・ヴォルテラ方程式とは
まずはロトカ・ヴォルテラ方程式がどういうものだったか思い出してみましょう。
\(\begin{eqnarray}\frac{{\rm d}x}{{\rm d}t} &=& \alpha x-\beta xy \\
\frac{{\rm d}y}{{\rm d}t} &=& \gamma xy-\eta y
\end{eqnarray}\)
方程式の意味は前回記事に書いたので割愛します。ここではとにかくこんな式だったよねと思い出すにとどめます。
→前回記事: ロトカ・ヴォルテラ方程式を解く
以下、変数\(t\)を消去した形、
\(\begin{eqnarray}
\frac{{\rm d}y}{{\rm d}x} = \frac{\gamma xy-\eta y}{\alpha x-\beta xy}
\end{eqnarray}\)
を考えます。
保存量を考える
まず保存量\(H\)とは以下のような方程式を満たすものを言います。
\(\begin{eqnarray}
\frac{{\rm d}H}{{\rm d}t} = 0
\end{eqnarray}\)
\(t\)は時間です。
ロトカ・ヴォルテラ方程式は変数分離形なので実は簡単に保存量を求めることができます。
なぜなら保存量\(H\)は
\(\begin{eqnarray}
{\rm d}H = \frac{\partial H}{\partial x}{\rm d}x+\frac{\partial H}{\partial y}{\rm d}y
\end{eqnarray}\)
を満たしますので各微係数\(\partial H/\partial x,\,\partial H/\partial y\)が求まれば良いですが、微分方程式が変数分離形であればある関数\(f\left(x\right)\)と\(g\left(y\right)\)を用いて
\(\begin{eqnarray}
f\left(x\right){\rm d}x = g\left(y\right){\rm d}y
\end{eqnarray}\)
のように書けるので
\(\begin{eqnarray}
H = \int f{\rm d}x-\int g{\rm d}y
\end{eqnarray}\)
と置けば
\(\begin{eqnarray}
{\rm d}H &=& f{\rm d}x-g{\rm d}y
&=& 0
\end{eqnarray}\)
のように\(H\)が保存量であることが示せるからです。
というわけで具体的にロトカ・ヴォルテラ方程式の保存量を考えてみましょう。
改めてロトカ・ヴォルテラ方程式に立ち返ります。
\(\begin{eqnarray}
\frac{{\rm d}y}{{\rm d}x} = \frac{\gamma xy-\eta y}{\alpha x-\beta xy}
\end{eqnarray}\)
変数分離形なので\(x\)を右辺に、\(y\)を左辺に集めましょう。
\(\begin{eqnarray}
\frac{{\rm d}y}{{\rm d}x} &=& \frac{y}{x} \frac{\gamma x-\eta}{\alpha-\beta y} \\
\frac{\alpha-\beta y}{y}{\rm d}y &=& \frac{\gamma x-\eta}{x}{\rm d}x \\
\left(\frac{\alpha}{y}-\beta\right){\rm d}y &=& \left(\gamma-\frac{\eta}{x}\right){\rm d}x
\end{eqnarray}\)
両辺積分して
\(\begin{eqnarray}
\alpha\log y-\beta y = \gamma x-\eta\log x
\end{eqnarray}\)
よって保存量\(H\)は
\(\begin{eqnarray}
H &=& \gamma x-\eta\log x-\alpha\log y+\beta y \\
&=& \gamma x+\beta y-\eta\log x-\alpha\log y
\end{eqnarray}\)
と導くことができました。
数値計算の結果
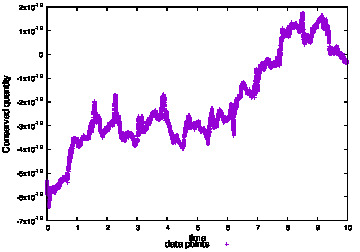
パラメータ\(\alpha = 8.0, \, \beta = 4.0,\, \gamma = 6.0,\, \eta = 18.0\)のときの保存量の時間変化は以下です。
 横軸: 時間、縦軸: 保存量の全時間平均からのずれ
横軸: 時間、縦軸: 保存量の全時間平均からのずれ
保存量の全時間平均からのずれが\(10^{-12}\)オーダなので保存則はきちんと保たれていると思います。
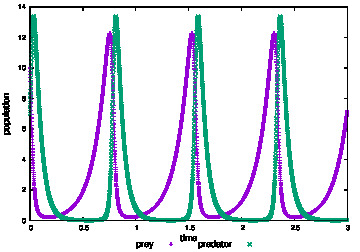
ちなみにこのときの各個体の時間変化は以下のようになっています。
 横軸: 時間、縦軸: population
横軸: 時間、縦軸: population
前回記事と定性的な傾向はそんなに変わってないですかね。
まとめ
今回はロトカ・ヴォルテラ方程式の保存量について書いてみました。
変数分離形の場合は保存量が簡単に導けることは結構応用範囲が広いんじゃないかと思います。
式の具体的な意味などは以下記事に書いたので合わせて読んでみて下さい!
この記事に関するご質問や、もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。