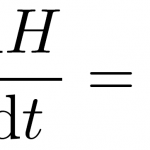今回はロトカ・ヴォルテラ方程式(Lotka-Volterra equation)で遊んでいきたいと思います。
ここではロトカ・ヴォルテラ方程式の概要を紹介した後、実際に数値的に解いてみた結果を紹介、パラメータをいじって遊んでみた結果を考察してみようと思います!
Lotka-Volterra equation
LV方程式は次のような形をしています。
LV方程式は自然界の食う・食われるをモデル化した方程式です。
ここではわかりやすいように、ライオンとシマウマで考えてみましょう。
\(x\)は食われる側(シマウマ)の個体数、\(y\)は食う側(ライオン)の個体数を表しています。
第1の方程式
を考えてみましょう。左辺は\(\frac{{\rm d}x}{{\rm d}t}\)なので単位時間にどのくらいシマウマの個体数が変化するかを表しています。
右辺の\(\alpha x\)の項はシマウマの数に比例して個体数が増えるということを意味しています。つまり、シマウマはたくさんいた方が繁殖しやすいということです。
\(\beta xy\)の項は捕食による個体数の減少を表しています。負号は減少という意味ですね。ライオンが多いほどシマウマは捕食されます。
また、シマウマが多くてもライオンは捕食しやすいです。つまり、シマウマの個体数減少につながるわけですね。
このようにLV方程式は自然界の弱肉強食の様子を微分方程式の形で表現したものなんですねぇ。
第2の方程式の意味は、みなさん自身で考えてみて下さい。
数値的に解いてみる
LV方程式は残念ながら解析的には解けません。
いつものように数値解析を使って解いてみましょう。
実装はcでやりました。
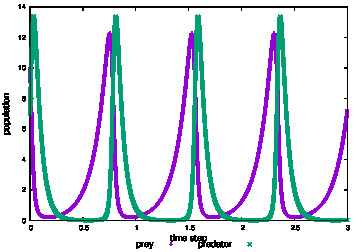
きれいに出ました。めちゃめちゃうれしいです。
このときのパラメータは\(\alpha=8.0,\,\beta=4.0,\,\gamma=6.0,\,\eta=18.0\)です。
緑色の点がライオン(捕食者)、紫の点がシマウマ(被捕食者)です。
最初はシマウマが減ってライオンが増えていきます。
しかしシマウマがある一定以上減ってくると、今度はライオンも減ってきます。
ライオンが減ってくると、シマウマが段々復活してきてまたライオンが捕食できるようになります。
するとまたシマウマが減って…
ということを繰り返していくという解になっています。
定性的にはこんな感じの解になります。
生態系の崩壊
ちなみにパラメータをいじると、その生態系を崩壊させ絶滅に追い込むこともできます。
無慈悲です。
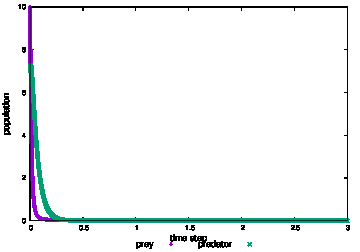
\(\alpha<0\)というのは、外的な要因(人間による乱獲など)によるシマウマの個体数の減少を方程式に導入したことと等価です。つまり人間の乱獲による個体数の減少を\(\zeta x\)という項で表して
シマウマの繁殖力の指標\(\alpha\)より人間による乱獲の多さの指標\(\zeta\)が大きいと右辺大一項の係数が負になってしまい、生態系の絶滅を引き起こすというモデル上の説明ができます1。
まとめ
いかがだったでしょうか。
今回はLotka-Volterra 方程式を解いてみました。
今後もいろいろと遊べそうなので、遊んでいきたいと思います。
[2022.9.22. 追記]
Lotka-Volterra方程式の満たす保存則についても書きました!
興味のある方は読んでみて下さい!
最後まで読んでいただきありがとうございました!!
他にも色々とシミュレーション関連の記事は書いていますので読んでみてください!
ライオンとシマウマの画像は無料画像提供サイトPixabayさんからダウンロードしています。いつもありがとうございます!!
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。