10秒で思い出す!回転行列の思い出し方

今回は回転行列をその場で簡単に思い出すテクニックについてご紹介したいと思います！

回転行列、ややこしいですよね。
どっかにマイナスがついてたんだけどどこだっけ？
cosとsinどういう順番だったっけ？
とか。
院試などその場で思い出さなければならなくなったとき、いちいち証明して安心する時間はありません。
またいちいち調べるのもそれはそれで面倒です。

そのような方のために、一度覚えておけば忘れない、簡単に回転行列を思い出す方法をご紹介します！

実用的には2次元くらいで十分だと思いますが、極座標の定義の仕方によっては任意の次元で適用可能だと思います。

復習
回転行列って何だっけ？
極座標
三角関数の加法定理
本論
1. 平面上の点を極座標成分に変換
2. 回転して元の成分と比較
まとめ

復習

回転行列って何だっけ？

まずは簡単に復習から。簡単のため2次元の\(xy\)座標系を考えることにします。

回転行列とは以下の行列で表される行列のことで、座標\(\left(x,y\right)\)を角度\(\alpha\)だけ回転したときに移される点\(\left(X,Y\right)\)と元の座標との関係を表したものです。

\(\begin{equation} {\bf X} = \left( \begin{array}{cc} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{array} \right) {\bf x} \end{equation}\)

ただし、\({\bf X} \equiv \left(X,Y\right)^{{\rm T}}\)、\({\bf x} \equiv \left(x,y\right)^{{\rm T}}\)と置きました。

\(\sin\)とか\(\cos\)で書かれている行列が回転行列です。
符号がややこしいです。
今回はこれを簡単な検算によって安心して使うテクニックのご紹介です。

極座標

今回ご紹介するテクニックは極座標を使うのでこれも簡単に復習しておきます。

\(xy\)座標系における極座標とは原点からの距離\(r\)と始線(\(x\)軸の正の向き)との角度\(\theta\)によって平面上の点を表す方法です。

\(xy\)座標系の成分\(\left(x,y\right)\)を以下のように変換することで極座標での表し方を得ます。

\(\begin{eqnarray} x &=& r\cos\theta \\ y &=& r\sin\theta \end{eqnarray}\)

ベクトルで書くと基底\({\bf e}_{x},\,{\bf e}_{y}\)を使って

\(\begin{eqnarray} {\bf r} &=& x{\bf e}_{x} + y{\bf e}_{y} \\ &=& r\cos\theta{\bf e}_{x}+r\sin\theta{\bf e}_{y} \end{eqnarray}\)

と書きます。

三角関数の加法定理

復習はこれで最後です。

証明は略しますが三角関数の加法定理を使うので結果だけ載せておきます。

\(\begin{eqnarray} \sin\left(\theta+\alpha\right) &=& \sin\theta\cos\alpha + \cos\theta\sin\alpha \\ \cos\left(\theta+\alpha\right) &=& \cos\theta\cos\alpha – \sin\theta\sin\alpha \end{eqnarray}\)

本論

以上の知識をもとに回転行列の簡単な思い出し方をご紹介します。
と言っても回転を愚直に扱うだけですが笑

大体以下のような流れです。

平面上の点を極座標成分に変換
回転して元の成分と比較

1. 平面上の点を極座標成分に変換

まずは平面上の点を極座標成分に変換します。

\(\begin{eqnarray} x &=& r\cos\theta \\ y &=& r\sin\theta \end{eqnarray}\)

2. 回転して元の成分と比較

次にこの点を角度\(\alpha\)だけ回転することを考えます。

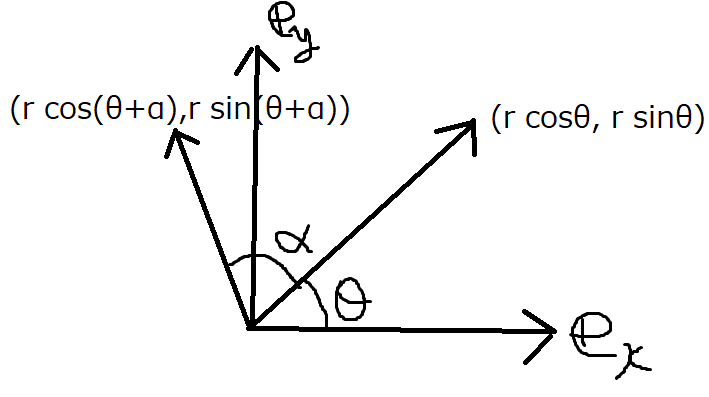
便宜的に回転前の座標成分を\({\bf x}\)、回転後の座標成分を\({\bf X}\)と書きます。

\({\bf X}\)を加法定理で展開することで回転行列の表現を得ます。

\(\begin{eqnarray} X &=& r\cos\left(\theta+\alpha\right) \\ &=& r\cos\theta\cos\alpha-r\sin\theta\sin\alpha \\ &=& x\cos\alpha-y\sin\alpha \\ Y &=& r\sin\left(\theta+\alpha\right) \\ &=& r\sin\theta\cos\alpha + r\sin\alpha\cos\theta \\ &=& y\cos\alpha + x\sin\alpha \end{eqnarray}\)

すなわち

\(\begin{eqnarray} {\bf X} = \left( \begin{array}{cc} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{array} \right) {\bf x} \end{eqnarray}\)

まとめ

いかがだったでしょうか。

今回は回転行列の簡単な思い出し方をご紹介しました。
三角関数の加法定理さえ覚えておけば回転行列は簡単に検算することが出来ます。
個人的には加法定理は覚えてられるのでこういうやり方で回転行列を思い出すことにしています。

もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。

tsunetthi(at)gmail.com

(at)の部分を@に変えてメールをお送りください。

または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。

サムネイル画像はpixabayさんからダウンロードさせていただきました！
ありがとうございます！