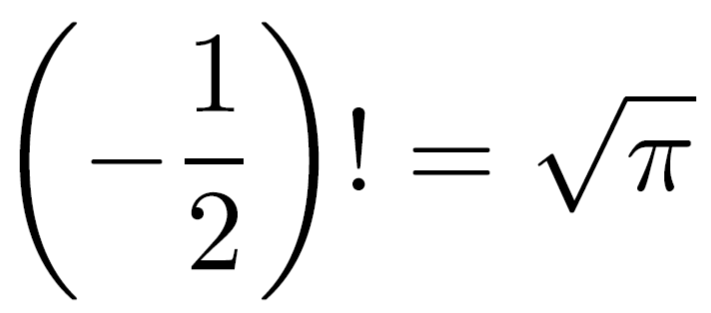今回は特殊関数の一つ、\(\Gamma\)関数について書いていこうと思います。
なんか唐突に書きたくなってしまったので。
ここでは特殊関数ってそもそも何?という話から始めて階乗の一般化としてガンマ関数を定義し、具体例として\(\left(1/2\right)!\)を計算してみようと思います!
大学のレポートなどにひょっとしたら役立つことが書いてあるかもしれません。
計算過程などもなるべく省略せずに書いていこうと思います。

私はもともと特殊関数というものが好きでした。
大学の授業を受けているうちに手書きの数式のカッコよさが気に入ってしまったんですね。
それで色々な数式をいじることに青春をささげた時期もありました。
今はMathematicaというソフトがその辺を自動でやってくれますが、個人的には途中の計算も自分でやっていきたい派です。非効率ですが飽きが来ないうちは案外楽しいものです。趣味程度にやってみてね。
今回は以下のような流れで進めていきます。いつも通り、ご自分の興味に合わせて読んでみて下さい!
そもそも特殊関数って何???
さて、そもそも特殊関数って何でしょう?
明確な定義は知りませんが、一般的には高校で習うような初等関数(sin とかcos とか exp など)で表すことのできない関数たちのことを言うようです。
有名どころでいくと円筒座標でよく出てくる Bessel 関数や水素原子の問題で出てくる Laguerre 陪関数などがあります。あとは今回の\(\Gamma\)関数も特殊関数の一つです。
特殊関数はそれはそれはたくさんありますが、実はいくつかについては、ある一つの関数(例えば合流型超幾何関数: Hypergeometric function of confluent type)から生まれることが分かっています。さらに特殊関数たちの満たす微分方程式を見つけるアルゴリズムがあることも分かっています。(この話はまたの機会に…)
一時期そういう関数たちの満たす微分方程式を見つけるのが流行って、いちいち名前をつけていたのですが、一挙にみつかるアルゴリズムの発見によりそういうことはなくなってしまいました。
時代が違えば流行りも違うものですねぇ。
\(\Gamma\)関数って何???
さて今回の本題に入ります。
\(\Gamma\)関数とは階乗を一般化したものです。

階乗というのは高校でも習う通り、ある自然数\(n\)から1までの数字を全てかけたものですね。すなわち
を「\(n\)の階乗」といいます。簡単ですね。例えば \(3!=3\cdot 2\cdot 1 = 6\)です。
自然数で定義できたら、もう少し範囲を広げて有理数まで階乗を定義したいと思うのは自然でしょう(負の整数ではないw)。
高校生の方はこの辺で混乱すると思いますが、\(\left(\frac{1}{2}\right)!\)を計算したいという衝動に駆られることがまぁあります。「2分の1の階乗」です。
なんじゃそれ、と思うかもしれませんが人生色々あるのでそういうこともあるのです。1
そういうときのために階乗を「自然数の階乗を含むように一般化」2します。
実用的には以下の積分の形でお目にかかることが多いです。実際には結果として階乗の表現になっていると言った方が理解に困らないでしょう。
一般に\(z\)は複素数と考えます。この定義が自然数の階乗を含んでいることを確認するために\(z=n\)\(\left(n\in\mathbb{N_{\geq 3}}\right)\)として部分積分を実行すると
ただし、\(n\)を3以上の自然数としているので2行目の表面項が落ちていることに注意してください。3このように続けていくと最後は\(\Gamma\left(1\right)\)までくることが予想されます。ここで具体的に\(\Gamma\left(1\right)\)の値を計算してみると
よって \(\Gamma\left(n\right)=\left(n-1\right)\left(n-2\right)\cdots 2\cdot 1=\left(n-1\right)!\) が示されました。すなわち先ほどの積分による\(\Gamma\)関数の定義は自然数の階乗を含んでいたのです。これを一般化して複素数\(z\)に対して”階乗”を
と定義することにしましょう。
\(\left(\frac{1}{2}\right)!\)を計算してみよう!
さて、それでは\(\left(\frac{1}{2}\right)!\)を計算してみましょう。先ほどの\(\Gamma\)関数の定義から
実はこの積分は非常に有名な「Gauss積分」というものです。4すなわち、\(t=x^{2}\)という変数変換によって\({\rm d}t=2x{\rm d}x\)に注意すれば
ゆえに
整数の世界からちょっと踏み出しただけで円周率\(\pi\)と遭遇してしまいました。不思議ですねぇ。

まとめ
いかがだったでしょうか。
本当は\(\beta\)関数や\(\zeta\)関数との関連も書きたかったのですが、記事のボリュームがすごいことになっちゃうのでやめました。
いかんせん、大学以降の数学は楽しいよということが伝えたかったことの一つでもあります。
いろんなことがつながっているんだなぁと実感すると思います。
最後まで読んでいただきありがとうございました!!
他にも色々と数学に関する記事を書いています。参考にしてみて下さい!
→「数学」一覧
また、\(\Gamma\)関数は別の特殊関数である\(\beta\)関数とも関わりがあります。これについても記事にしたので良かったら読んでみて下さい!
→ベータ関数~ガンマとのつながりにおいて~
こちらで使わせていただいている一部の画像は無料画像提供サイトPixabayさんからダウンロードしています。いつもありがとうございます!!
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。