今回はエネルギー保存則を使って具体的な問題を解いてみたいと思います1!
エネルギー保存がどういうものかよくわからない方は
を読んで参考にしてみてください!
今回は以下のような流れで説明していきます。
また、高校物理に関する記事は以下にまとめてあります。
→「高校物理」一覧
他の記事も読んでみて下さい!
問題設定
今回は分かりやすいように、前回考えた振り子を考えてみましょう2。
関連記事: 高校物理のお話~エネルギー保存 (基礎編)~
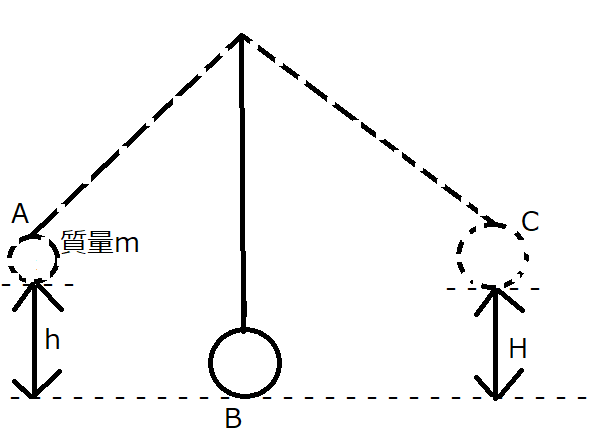
Aの位置まで振り子を持ち上げて、そっと手を放します。「そっと」というのは「初速度0で」ということです。
Bの点線の位置を基準として、高さ\(h,\,H\)の位置をA,C としています。
前回の話だと、\(h=H\)のはずですが、今回は一応知らないふりをして本当に同じ高さになるかを検証してみましょう。
関連記事: 高校物理のお話~エネルギー保存 (基礎編)~
問題1~力学的エネルギーが保存しているとAとCの高さは同じになるか~
力学的エネルギー保存則を信じるとAの位置でもCの位置でも力学的エネルギーは同じ値です。そこでAの位置とCの位置の力学的エネルギーを考えてみます。
力学的エネルギー\(E\)というのは、その状態での運動エネルギー\(K\)と位置エネルギー\(U\)の和
のことでしたね。
さて、高さ\(y\)の位置にある質量\(\mathcal{M}\)の物体がもつ位置エネルギーは
ですね。(重力に逆らって高さ\(y\)まで持ち上げるのに必要な仕事です。これについてはまた別の記事でご説明しようと思います。今回はそういうもんだと思ってください。)
\(g\)は重力加速度です。
物体がAの位置にあるとき、質量\(m\)で高さは\(h\)なので位置エネルギーは
物体がCの位置にあるとき、質量\(m\)で高さは\(H\)なので
また、両方とも静止しているので、運動エネルギーは0です。
よってそれぞれの状態の力学的エネルギーは
となります。
力学的エネルギーの保存則を信じるとAの状態とCの状態の力学的エネルギーの値は一緒のはずなので
すなわち、
ということが、まぁ一応計算からわかるわけですね。
問題2~じゃあ初速があったらどうなのよ~
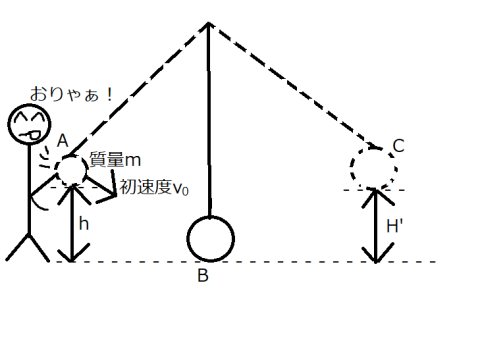
次はちょっと問題を変えて最初にそっと手を放すのではなくて3、
おりゃぁ!
とぶん投げた場合を考えます。
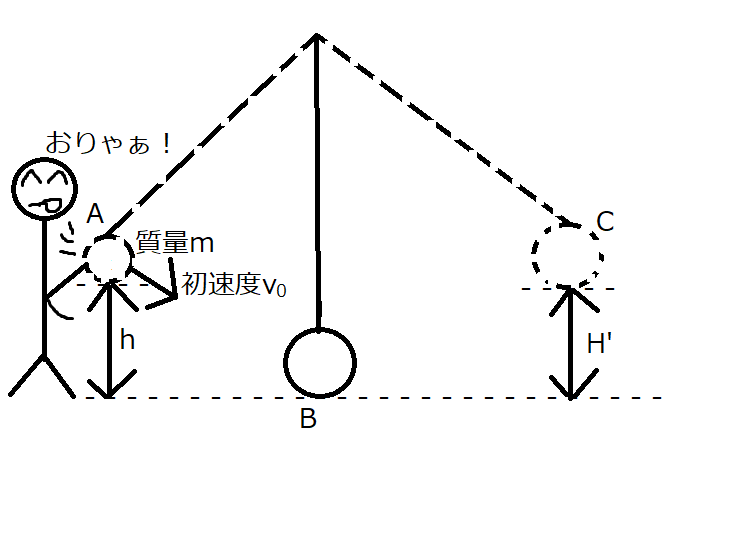
このとき振り子の静止するC点の高さ\(H’\)はどうなるでしょうか。
再び力学的エネルギー保存則を使って考えてみましょう。
まず、C点の力学的エネルギーは高さ\(H’\)なので
です。
さっきと違う状況なのはA点です。
さっきはそっと手を放したので初速度0でしたが、
今回はぶん投げているので初速度\(v_{0}\)がついてしまっています。
つまり、位置エネルギーだけでなく運動エネルギーも持っているわけですね。
質量\(\mathcal{M}\)で速度\(V\)を持つ物体の運動エネルギーは
と表されます4。
一方、高さは\(h\)ですから、Aの状態の力学的エネルギーは
力学的エネルギーの保存則を信じると、Aの状態の力学的エネルギーとCの状態の力学的エネルギーは一緒の値のはずですから
よって5
(実数)\(^2\)は正、すなわち\(\frac{1}{2g}v_{0}^{2}\geq 0\)なので
そっと手を放すより高く上がる6ということがわかり、その高さの増え方が初速度の2乗に従って増えていくということも分かりました。
まとめ
いかがだったでしょうか。
今回は
高校物理のお話~エネルギー保存 (基礎編)~
の知識を使って、具体的な問題に応用してみました。
次回は運動量保存のお話でもしましょうかね。
他にも色々と高校物理に関する記事を書いています。参考にしてください!
→「高校物理」一覧
もっとこんなことを記事にしてほしいなどのご要望がありましたら、このページ上部のお問い合わせフォームまたは下部のコメント欄からご連絡いただくか、以下のメールアドレスでもお待ちしております。
tsunetthi(at)gmail.com
(at)の部分を@に変えてメールをお送りください。
または、twitter(@warotan3)もやってますのでそちらに連絡していただいても良きです。