3 dimensional ball and story of my school life about study

Hello, guys! It’s me! Warotan!
So…Who are you?→ABOUT ME

This time, let’s calculate the volume of a 3 dimensional ball toward that of an \(n\) dimensional ball.
Also, my misunderstanding about study in high school is given.

I drunk too much today, so there might be some mistakes.
The year-end party was so much fun!!

I would like to tell you the construction of this page and please select where you start to read to your interests.

The volume of a 3 dimensional ball
Story of my school life~Integration is a method of calculating the area of a graph!?~
Summary

The volume of a 3 dimensional ball

We know that the volume of a 3 dimensional ball is written as

\(\begin{eqnarray}V_{3}=\frac{4}{3}\pi r^{3}.\end{eqnarray}\)

The suffix 3 shows that it is a THREE dimensional one.

How can we derive this formula?

Let us first consider a semicircle as a preparation for the 3 dimensional volume.

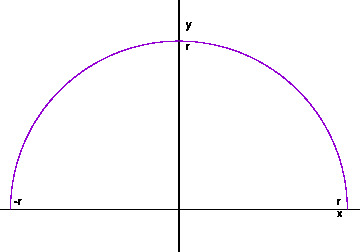
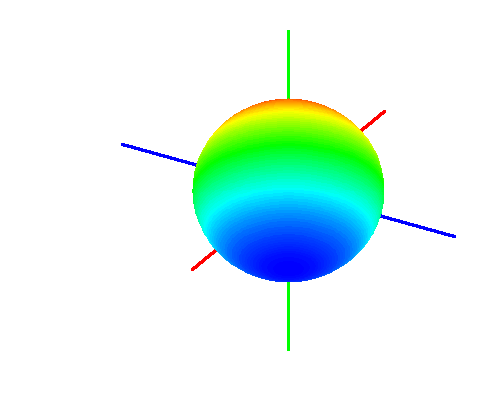
If we rotate this around the \(x\) axis, we can make a three dimensional ball.

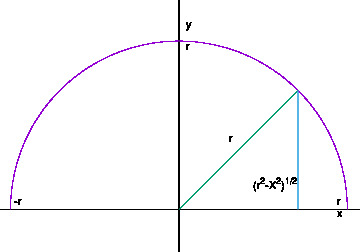
Rotating the semicircle around the axis, we get a 3 dimensional ball.

Rotating the blue line around the \(x\) axis, we get a circle of radius \(\xi \equiv \sqrt{r^2-X^2}\).

The area of a circle created by turning the blue line at \(X\) around the \(x\) axis is given by \(\pi \xi^2\), \(\xi \equiv \sqrt{r^2-X^2}\).
If we consider a disk of thickness \({\rm d}X\), the volume is \(\pi \xi^2{\rm d}X\).
Summing up this volume in \(X\in\left[-r,r\right]\) gives us the desired volume;

\(\begin{eqnarray} V_{3} &=& \int_{-r}^{r}\pi\xi^2 {\rm d}X \\ &=& \pi\int_{-r}^{r}\left(r^2-X^2\right){\rm d}X \\ &=& \pi \, 2\int_{0}^{r}\left(r^2-X^2\right){\rm d}X \\ &=& 2\pi\left[r^2X-\frac{1}{3}X^3\right]^{r}_{0} \\ &=& 2\pi\left(r^3-\frac{1}{3}r^3\right) \\ &=& 2\pi\frac{2}{3}r^3 \\ &=& \frac{4}{3}\pi r^3 \end{eqnarray}\)

It is a kind of shell integration.

Story of my school life~Integration is a method of calculating the area of a graph!?~

In addition to the main story, I tell you my mistake about study.

When I was a high school student, I was not (and am not so) good at studying.
One of my big misinterpretation was about integration.

In those days, I thought that integration is a method of calculating an area of a graph.
Exercises about integration given by the school was all to calculate an area such as
“calculate the area between \(y=-x^2+3\) and the \(x\) axis” or
“calculate the area between \(y=\sin\left(x\right)\,\left(0\leq x\leq \pi\right)\) and the \(x\) axis”
and so on…
I came to think that
Ah… ok. Integration gives us an area!

BUT!!! That was a mistake.
After I passed the entrance exam of a university and, in the lecture,
a professor wrote some equations like

\(\begin{eqnarray} M &=& \int{\rm d}m \\ &=& \int\rho{\rm d}V. \end{eqnarray}\)

Here \(M\) is mass and \(\rho\) is density.

It confused me and I got into a panic.
“What does it mean??? Integration gives me an area but he says he calculates the mass of something???”

Of course it’s impossible for one who thinks integration is a method of calculating an area to understand the equation.

Now that makes me laugh but I was serious and asked him what the equation means.
He was surprised but taught me so kindly.

Summary

Now, that’s all what I wanted to write.

This time, we did a warming up for the next step, volume of an \(n\) dimensional ball and I gave you a story of my school study.
Dividing a large problem into small ones is a usual practice (integration).

Thank you for reading and please spread this blog if you like.

If you have any comment, please let me know from the e-mail address below or the CONTACT on the menu bar.
tsunetthi(at)gmail.com
Please change (at) to @.

Or you can also contact me via twitter (@warotan3)